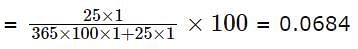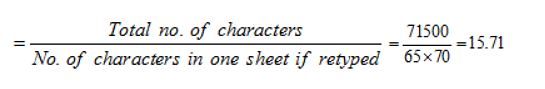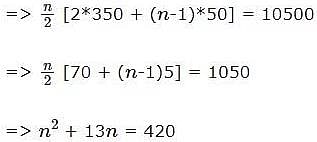Practice Test: Percentages - 1 - UPSC MCQ
10 Questions MCQ Test CSAT Preparation - Practice Test: Percentages - 1
Instead of a metre scale, a cloth merchant uses a faulty 120 cm scale while buying, but uses a faulty 80 cm scale while selling the same cloth. If he offers a discount of 20%, what is his overall profit percentage?
Sailesh is working as a sales executive with a reputed FMCG Company in Hyderabad. As per the Company’s policy, Sailesh gets a commission of 6% on all sales upto Rs. 1,00,000 and 5% on all sales in excess of this amount. If Sailesh remits Rs. 2,65,000 to the FMCG company after deducting his commission, his total sales were worth:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
The ratio of number of male and female journalists in a newspaper office is 5:4. The newspaper has two sections, political and sports. If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
If equal numbers of people are born on each day, find the approximate percentage of the people whose birthday will fall on 29th February. If we are to consider people born in 20th century (1901-2000) and assuming no deaths.
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
A person who has a certain amount with him goes to market. He can buy 50 oranges or 40 mangoes. He retains 10% of the amount for taxi fares and buys 20 mangoes and of the balance, he purchases oranges. Number of oranges he can purchase is:
A report consists of 20 sheets each of 55 lines and each such line consists of 65 characters. This report is reduced onto sheets each of 65 lines such that each line consists of 70 characters. The percentage reduction in number of sheets is closest to:
Seema has joined a new Company after the completion of her B.Tech from a reputed engineering college in Chennai. She saves 10% of her income in each of the first three months of her service and for every subsequent month, her savings are Rs. 50 more than the savings of the immediate previous month. If her joining income was Rs. 3000, her total savings from the start of the service will be Rs. 11400 in:
|
218 videos|139 docs|151 tests
|