Practice Test: Seating Arrangement - 1 - UPSC MCQ
10 Questions MCQ Test CSAT Preparation - Practice Test: Seating Arrangement - 1
Which of the arrangements done by Mr. Crazy is not consistent with the information stated under "Additional Information"?
Which of the following persons is wearing a blue shirt?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following persons is wearing a green shirt?
Which of the following is not a permissible group of four persons such that the number of persons wearing a red, a green and a blue shirt is 2, 1 and 1 respectively?
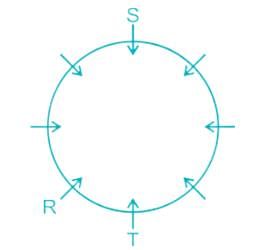
These questions are based on the following information. P, Q, R, S and T sit around a table. P sits two seats to the left of R and Q sits two seats to the right of R.
Q. If S sits in between Q and R, who sits to the immediate right of P?
These questions are based on the following information. P, Q, R, S and T sit around a table. P sits two seats to the left of R and Q sits two seats to the right of R.
Q. Which of the following cannot be the correct seating arrangement of the five persons in either the clockwise direction or the anti-clockwise direction?
These questions are based on the following information. P, Q, R, S and T sit around a table. P sits two seats to the left of R and Q sits two seats to the right of R.
Q. If S is not sitting next to Q, who is sitting between Q and S?
These questions are based on the following information. P, Q, R, S and T sit around a table. P sits two seats to the left of R and Q sits two seats to the right of R.
Q. If a new person U joins the group such that the initial conditions for the seating arrangement should be observed and also a new condition that U does not sit next to R be satisfied, then which of the following statements is true?
These questions are based on the following information. P, Q, R, S and T sit around a table. P sits two seats to the left of R and Q sits two seats to the right of R.
Q. If a new person U joins the group such that the initial conditions for the seating arrangement should be observed and also a new condition that U does not sit next to P, S or T be satisfied, then who will be the neighbours of P (one on either side)?
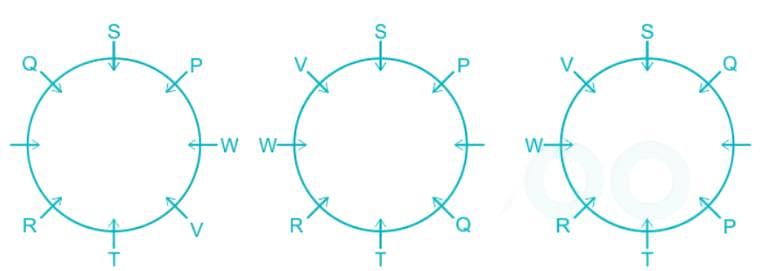
Eight persons P, Q, R, S, T, U, V and W are sitting around a circular table facing the center (not necessarily in the same order). Two persons sit between Q and W. V sits immediate left of W. Three persons sit between S and T. R sits immediate left of T. U is not the neighbor of P. One person sits between P and Q.
Which of the following statement is correct?
|
218 videos|139 docs|151 tests
|