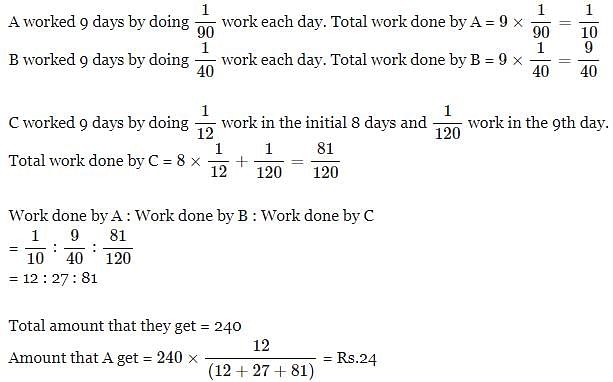Practice Test: Time & Work- 2 - UPSC MCQ
20 Questions MCQ Test CSAT Preparation - Practice Test: Time & Work- 2
Mayank can do 50% more work than Shishu in the same time. Shishu alone can do a piece of work in 30 hours. Shishu starts working and he had already worked for 12 hours when Mayank joins him. How many hours should Shishu and Mayank work together to complete the remaining work?
A can do a piece of work in 90 days, B in 40 days and C in 12 days. They work for a day each in turn, i.e., first day A does it alone, second day B does it alone and 3rd day C does it alone. After that the cycle is repeated till the work is finished. They get Rs 240 for this job. If the wages are divided in proportion to the work each had done. Find the amount A will get?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Read the passage below and solve the questions based on it.
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
Q. What is the volume of the tank?
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
Read the passage below and solve the questions based on it.
There are three taps A, B and C and an outlet pipe D. A, B and C can fill the tank in the Panikam locality in 10, 20 and 25 h respectively. The outlet pipe can empty the same tank in 100 h. There are 2,000 houses in the locality. The tank has a capacity of 50,000 litres
Q.
If all the taps and the outlet pipe are opened simultaneously, how much water is thrown into the tank every hour?
There are three taps A, B and C in a tank. They can fill the tank in 25 hrs, 20 hrs and 10 hrs respectively. At first all of them are opened simultaneously. Then after 1 hrs, tap C is closed and tap A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone.
Find the percentage of work done by tap A itself?
Anup can dig a well in 10 days. but particularly in difficult time the work is such that due to fatigue every subsequent day efficiency of a worker falls by 10%.If Anup is given a task of digging one such well in the difficult time, then in how many days will he finish the work?
A and B together can complete a work in 3 days. They start together but after 2 days, B left the work. If the work is completed after two more days, B alone could do the work in
Refer to the data below and answer the questions that follow.
Anoop was writing the reading comprehension sections in the DOG entrance examinations. There were four passages of exactly equal length in terms of the number of words, and the four passages had 5, 8, 8, and 6 questions following each of them, respectively. It is known that Anoop can answer exactly 12 questions in the time he takes to read any one of the four passages. Assume that his rate of reading and answering questions remains the same throughout the section.
Q.
By what per cent should Anoop increase his reading speed if he has to cut down on his total time spent on the section by 20%? Assume that the time spent on answering the questions is constant and as given in the directions.
A can work twice as fast as B. A and C together can work thrice as fast as B. If A, B and C complete a job in 30 days working together, in how many days can each of them complete the work?
In what time would a cistern be filled by three pipes of diameter of 1 cm, 2 cm and 3 cm if the largest pipe alone can fill the cistern in 49 minutes, the amount of water flowing through each pipe being proportional to the square of its diameter?
Sagar is 20% more efficient than Pranesh. If Pranesh can complete a piece of work in 30 days, then in how many days can both Sagar and Pranesh complete the work?
A factory manufactures dyes. It has 12 men and two machines which can be operated by all of its men. It takes 4 hours to manufacture one dye on the machine with the operator. The machines can work continuously without a break. Without the machine each of the men can manufacture a dye in 8 hours. The policy is such that the production is maximized and the men are ready to work in three shifts of 8 hours per day. What will be the average cost incurred per dye if 1 man hour costs Rs 20 and 1 machine hour costs Rs 15?
480 persons working 10 hours per day complete one-fourth of a work in 10 days. How many additional persons are to be employed in order to complete the remaining work in 20 days, working 8 hours per day?
Anil, Bhuvan and Chandan take 10,20 and 25 days to complete a job. What is the minimum time required to finish the job if not more than 2 of them work together on a single day and no two consecutive days have the same pair of people working?
Anuj can do a piece of work in a certain number of days. To do the same piece of work, Bhanu takes thrice the number of days as Anuj takes whereas Chandu takes thrice as many days as Bhanu does and Dodo takes thrice as many days as Chandu does. Now, they are paired and two groups are formed. The first pair takes one-third the time taken by the second pair to complete the work, which is the first pair?
Two pipes can separately fill a tank in 20 hours and 30 hours respectively. Both the pipes are opened to fill the tank but when the tank is 3/4th full, a leak develops in, through which one-fourth of water supplied by both the pipes goes out. What is the total time taken to fill the tank?
A tank can be filled in 30 minutes by 20 pumps. If five pumps go out of order, what time will be taken by the remaining pumps?
In a military camp there is sufficient food supply for 200 soldiers for 40 days. After 10 days, certain number of men join and everyone eats 50% more than earlier. Now the food lasts for another 10 days. How many soldiers joined the camp after 10 days?
A man, a woman or a boy can do a job in 20 days, 30 days or 60 days respectively. How many boys must assist 4 men and 5 women to do the work in 2 days?
Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is
|
218 videos|139 docs|151 tests
|



 .
.