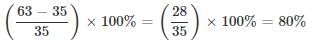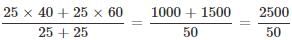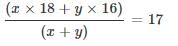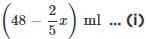GRE Mock Test (New Pattern) - 2 - GRE MCQ
30 Questions MCQ Test - GRE Mock Test (New Pattern) - 2
One element, which may not justify violence itself but which __________ its use, is the belief that death in a sacred cause is the proper end of life.
Directions: For each sentence, choose one word for each set of blanks. Select the word or words that best fit(s) the meaning of the sentence as a whole.
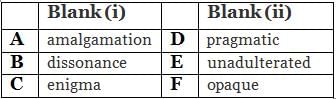
Q. The (i) _______ relationship between patients and their doctors is evidenced by patients’ (ii) _____ reactions to the attempts by insurance companies to force patients to see new doctors in different health care networks.


Directions: For each sentence, choose one word for each set of blanks. Select the word or words that best fit(s) the meaning of the sentence as a whole.
Q. It was apparent that the recordings were ________ remastered, as the vocals were barely audible through the wave of noise.
Directions: For each sentence, choose one word for each set of blanks. Select the word or words that best fit(s) the meaning of the sentence as a whole.
Q. While the guitar has (i) _____ over the course of its centuries-long history, perhaps most notably with the invention of the electric guitar in the 1930s, the modern guitar exhibits (ii) _____ the vihuela of 15th-century Spain. A skilled guitarist would likely be able to pick up this (iii) _____ instrument, also an ancestor of the viol, andcompetently play a tune.

Directions: For each sentence, choose one word for each set of blanks. Select the word or words that best fit(s) the meaning of the sentence as a whole.
Q. The punctilious wine aficionado was a consummate purist when it came to his tastes. He immediately rejected the (i) _______ of two wines. As an alternative, and as a generalrule, he preferred a simple, (ii) ______ wine.
Directions: Read the following passage and answer the question.
All artists are reputed to suffer to some degree for their art, but some may physically suffer more than others. As part of The 3rd I project, a performance artist agreed to have a camera surgically implanted into the back of his head and the footage gathered from the experiment to be uploaded hourly into a website. The surgery involves slicing and lifting folds of skin and implanting the camera into the back of the skull and is excruciating for the artist. Some critics claim that the visceral reaction of hearing about the camera or its insertion may be orchestrated to shock viewers into learning more about the art or the project. Although the camera can be fitted with a lens cap to protect the privacy of those who request it, every single detail of the artist’s life is recorded and open for all to view. One might conclude that this project is an extreme example of the Modernists’ tendency to take the creation of art as its subject.
Q. The passage implies that the strength of the reaction the artwork evokes would be substantially weakened if which of the following were to happen?
In the figure shown below, line segment BC has length 16 cm, rectangle FABE is a square, and the area of rectangular region FACD is 612 cm2.
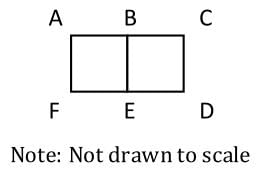
Quantity A
Area of FABE
Quantity B
Area of EBCD
Working independently, Machine A can complete a work in 3.5 hours, while Machine B can complete the same work in x hours. Working simultaneously, they together complete the same work in 1.5 hours.
Quantity A
3
Quantity B
x
A driver completed the first 20 miles of a 40-mile trip at an average speed of 50 miles per hour and the second 20 miles at an average speed of x miles per hour. The average speed for the entire 40-mile trip was 60 miles per hour. (Assume that the driver did not make any stops during the 40-mile trip.)
Quantity A
x − 60
Quantity B
10
If the roots of the equation x2 − 16x − 612 = 0 are a and b, what is the value of a + b?
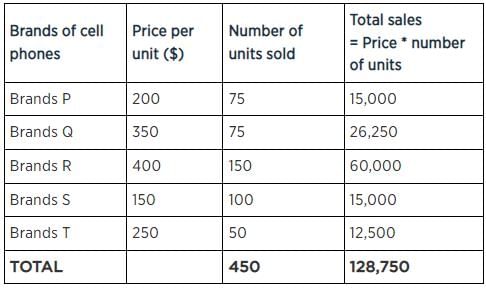
At a certain store for a certain month, in a chart given below, the price per cell phone (in dollars) is shown by dots (read from right hand side vertical axis) and the number of cell phones sold (read from left hand side vertical axis).
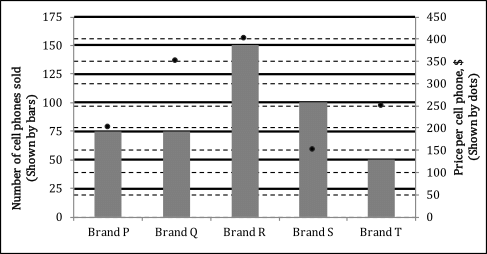
Q. What is the median price of the cell phones sold by the store in that month?
At a certain store for a certain month, in a chart given below, the price per cell phone (in dollars) is shown by dots (read from right hand side vertical axis) and the number of cell phones sold (read from left hand side vertical axis).
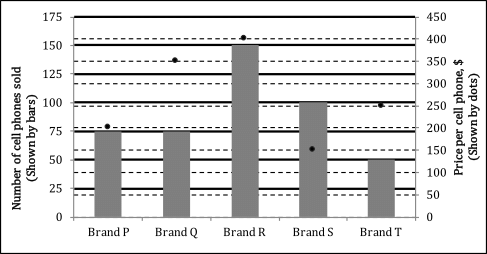
Q. What is the mean price (nearest to a dollar) of the cell phone sold by the store in that month?
If x is an integer, how many possible values of x satisfy the equation: (x−2)2(x+1) = 1
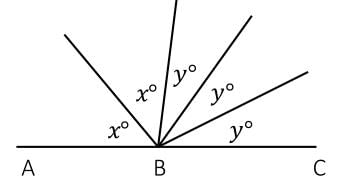
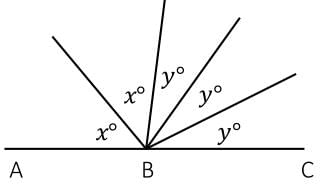
If ABC is a straight line as shown in the figure below, and the angles x & y are integer multiples of 20, what is the value of x?
Suzy purchased at least one pen priced at $13 each and at least one notebook priced at $19 each. If the total price of the items purchased is $58, what is the total number of pens and notebooks purchased by Suzy?
What could be the values of integers from 180 to 300, inclusive, that leave the remainder 2 when divided by 15 and by 9?
Indicate all such numbers.
[ Note: Select one or more answer choices ]
The sequence a1,a2,a3,…an,… is such that a1 = −2, a2 = −5, a3 = 4, a4 = 3, and an = an−4 for n >4.
Quantity A
The sum of the first 64 terms of the sequence
Quantity B
The sum of the first 98 terms of the sequence
3, a, 1, 9, b, 3
The arithmetic mean of the list of numbers above is 4 and a and b are integers.
Quantity A
Median of the list
Quantity B
Mean of the list
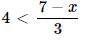
Quantity A
Maximum value of −(5 − x)
Quantity B
Maximum value of 2x
If the length and the breadth of a rectangle each is a prime number less than 11, and the perimeter of the rectangle is less than 24 unit, which of the following could be the possible value of the area?
Indicate all such areas.
[ Note: Select one or more answer choices ]
David bought greater than 10 paperback books that cost $8 each and greater than 8 hardcover books that cost $20 each. If the total cost of all the books that he bought was between $240 and $300, exclusive, how many total number of books could he buy?
Indicate all such answers.
[ Note: Select one or more answer choices ]
The following chart shows the percent distribution of the number of candidates enrolled in a certain test-prep company from 2014 to 2017 for four courses: GMAT, GRE, SAT and LSAT.
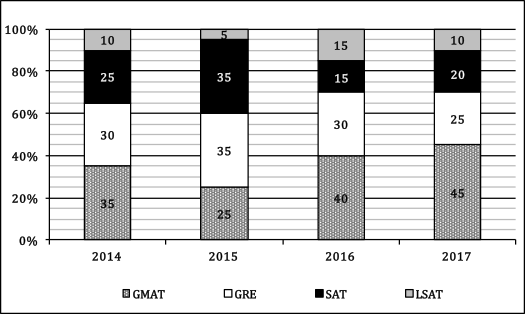
Q. If the total number of candidates increased by 40% from the year 2014 to the year 2017, what is the simple annual percent increase (if necessary whole number rounded) in the number of candidates for the GMAT course between 2014 and 2017?
The following chart shows the percent distribution of the number of candidates enrolled in a certain test-prep company from 2014 to 2017 for four courses: GMAT, GRE, SAT and LSAT.
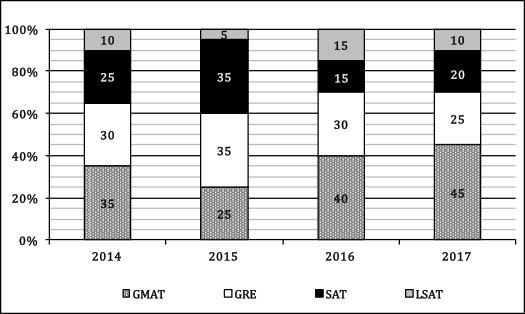
Q. If the number of candidates in 2014 was 500, and there was a 20% increase in the number of candidates per year for the next two years, what is the number of candidates for the LSAT course in 2016?
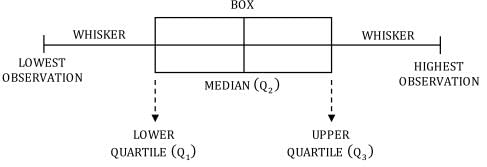
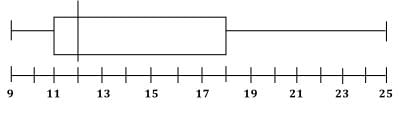
The box-and-whisker plot above shows weights for 60 kids in a playgroup. How many kids weight between 18 kilograms and 23 kilograms, inclusive, if the 23 kilograms represents the 90th percentile value on the plot above?
In a certain batch of guests in a museum, there are 50 guests; each guest buys either a $40 ticket or a $60 ticket, with at least one guest of each ticket type. The average (arithmetic mean) value of ticket-receipts from the batch is more than $50. If the average value of ticket-receipts is to be reduced to less than $50 by including few new guests with $40 tickets, what could definitely NOT be the number of new guests with $40 tickets that could be included?
Indicate all such numbers.
[ Note: Select one or more answer choices ]
If two interior angles of a quadrilateral ABCD are right angles and the degree measure of ∠ABC is twice the degree measure of ∠BCD, what could be the measure of the largest interior angle of quadrilateral ABCD?
Indicate all such angles.
If a group of students having an average age of 16 years joined a class, the average age of all the students in the class reduces from 18 years to 17 years. What is the ratio of the number of students who joined the class to the number of students who were initially in the class?
A 120-milliliter mixture of Chemical X and water contained 40 percent Chemical X. A part of the mixture was removed and replaced with an equal quantity of water. If the resulting mixture contained 10 percent Chemical X, what is the volume of the mixture that was removed?
If x and y are non-negative integers such that 2x + 3y = 8 and z = x2 + y2, what is the maximum value of z?



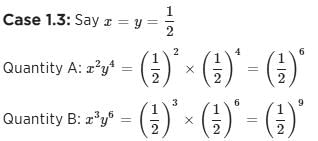
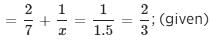
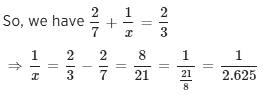
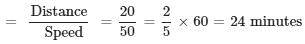
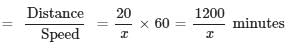
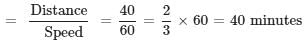
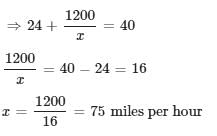
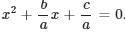 . Here, sum of the roots
. Here, sum of the roots 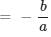 and the product of the roots = c/a.
and the product of the roots = c/a.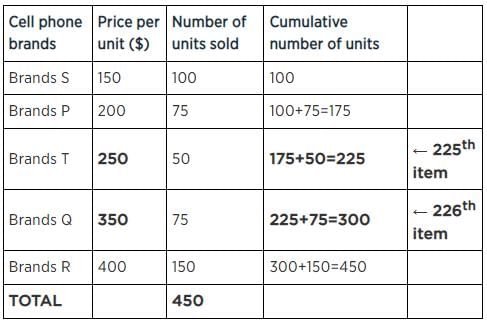
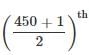
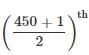 item/cell phone
item/cell phone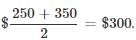
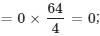 there would be 64/4 = 16 groups with each having their value equal to 0.
there would be 64/4 = 16 groups with each having their value equal to 0.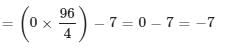
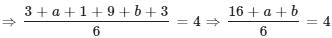
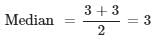
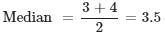
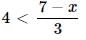
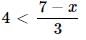
 24, the possible value of area = 5 × 7 = 35 is not possible.
24, the possible value of area = 5 × 7 = 35 is not possible.