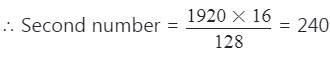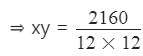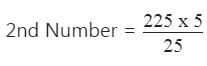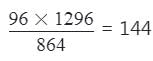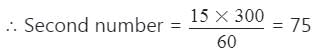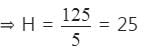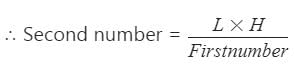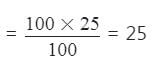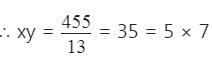MCQ: HCF और LCM - 1 - Bank Exams MCQ
15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - MCQ: HCF और LCM - 1
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।
दो संख्याओं का HCF 15 है और उनका LCM 225 है। यदि इनमें से एक संख्या 75 है, तो दूसरी संख्या क्या होगी?
तीन भिन्न संख्याओं का L.C.M. 120 है। निम्नलिखित में से कौन सा उनके H.C.F. नहीं हो सकता?
दो संख्याओं का गुणनफल 1280 है और उनका एच.सी.एफ. 8 है। उन संख्याओं का एल.सी.एम. क्या होगा?
दो संख्याओं का HCF और LCM क्रमशः 12 और 924 हैं। फिर ऐसी जोड़ों की संख्या क्या है?
दो संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। ऐसी संभव जोड़ों की संख्या क्या है?
दो संख्याओं का LCM 225 है और उनका HCF 5 है। यदि एक संख्या 25 है, तो दूसरी संख्या क्या होगी?
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?
दो संख्याओं का H.C.F. 96 है और उनका L.C.M. 1296 है। यदि एक संख्या 864 है, तो दूसरी संख्या क्या होगी?
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।
दो संख्याओं का HCF 15 है और उनका LCM 300 है। यदि एक संख्या 60 है, तो दूसरी संख्या क्या होगी?
दो संख्याओं का LCM उनके HCF का 4 गुना है। LCM और HCF का योग 125 है। यदि एक संख्या 100 है, तो दूसरी संख्या क्या होगी?
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?
दो संख्याओं का HCF और LCM क्रमशः 13 और 455 है। यदि इनमें से एक संख्या 75 और 125 के बीच है, तो वह संख्या क्या है?
दो संख्याओं का LCM 864 है और उनका HCF 144 है। यदि एक संख्या 288 है, तो दूसरी संख्या क्या होगी?
|
171 docs|185 tests
|