All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  Quantitative Aptitude/संख्यात्मक योग्यता  >  परीक्षा: ज्यामिति- 1 - Bank Exams MCQ

परीक्षा: ज्यामिति- 1 - Bank Exams MCQ


Test Description

15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - परीक्षा: ज्यामिति- 1

परीक्षा: ज्यामिति- 1 for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation. The परीक्षा: ज्यामिति- 1 questions and answers have been prepared according to the Bank Exams exam syllabus.The परीक्षा: ज्यामिति- 1 MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for परीक्षा: ज्यामिति- 1 below.
Solutions of परीक्षा: ज्यामिति- 1 questions in English are available as part of our Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams & परीक्षा: ज्यामिति- 1 solutions in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt परीक्षा: ज्यामिति- 1 | 15 questions in 30 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study Quantitative Aptitude/संख्यात्मक योग्यता for Bank Exams Exam | Download free PDF with solutions
परीक्षा: ज्यामिति- 1 - Question 1
Save

एक लंबा खड़ा棒, जिसकी लंबाई 20 मीटर है, जमीन पर 10 मीटर लंबी छाया डालता है। उसी समय, एक टॉवर जमीन पर 50 मीटर लंबी छाया डालता है। टॉवर की ऊँचाई ज्ञात करें।

Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 1

जब棒 की लंबाई = 20 मीटर है, तो छाया की लंबाई = 10 मीटर है, अर्थात् इस मामले में लंबाई = 2 * छाया

सूर्य के समान झुकाव के कोण के साथ, टॉवर की लंबाई जो 50 मीटर की छाया डालती है, है: 2 * 50 मीटर = 100 मीटर
टॉवर की ऊँचाई = 100 मीटर

परीक्षा: ज्यामिति- 1 - Question 2
Save

समान त्रिकोण, ABC और DEF का क्षेत्रफल क्रमशः 144 सेमी2 और 81 सेमी2 है। यदि बड़े त्रिकोण △ABC की सबसे लंबी भुजा 36 सेमी है, तो छोटे त्रिकोण △DEF की सबसे लंबी भुजा क्या होगी?

Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 2

समान त्रिकोणों में भुजाओं का अनुपात उनके क्षेत्रफलों के वर्गमूल के समान होता है। यहाँ, ABC का क्षेत्रफल 144 सेमी2 और DEF का क्षेत्रफल 81 सेमी2 है। अनुपात = √(144/81) = √(16/9) = 4/3।
इसलिए, यदि ABC की सबसे लंबी भुजा 36 सेमी है, तो DEF की सबसे लंबी भुजा = 36 × (3/4) = 27 सेमी।

Clear all your doubts with EduRev
परीक्षा: ज्यामिति- 1 - Question 3
Save

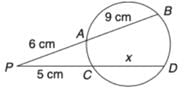
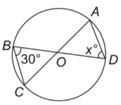
चित्र में x का मान ज्ञात कीजिए, यदि यह दिया गया है कि AC और BD वृत्त के व्यास हैं।

Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 3

त्रिकोण BOC एक समद्विबाहु त्रिकोण है जिसमें OB और OC की भुजाएं समान हैं क्योंकि वे वृत्त के त्रिज्याएँ हैं। इसलिए, कोण OBC = कोण OCB = 30°।

अतः त्रिकोण BOC का तीसरा कोण यानी कोण BOC 120° के बराबर होगा।
⇒ BOC = AOD = 120° 

इसके अलावा, समद्विबाहु त्रिकोण DOA में:
कोण ODA = कोण DAO = x = 30°

परीक्षा: ज्यामिति- 1 - Question 4
Save

दी गई आकृति में x का मान ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 4

स्पर्श रेखाओं के नियम द्वारा, हमें मिलता है:

⇒ 122 = (x + 7)x
⇒ 144 = x2 + 7x
⇒ x2 + 7x – 144 = 0
⇒ x2 +16x – 9x –144 = 0
⇒ x(x + 16) – 9(x + 16) = 0
⇒ x = 9 या –16

–16 लंबाई नहीं हो सकता, इसलिए इस मान को त्याग दिया जाता है। इसलिए, x = 9

परीक्षा: ज्यामिति- 1 - Question 5
Save

दी गई आकृति में x का मान ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 5

तारों के नियम के अनुसार, बाहरी कटाव द्वारा हम प्राप्त करते हैं:

(9 + 6) * 6 = (5 + x) * 5
90 = 25 + 5x
5x = 65
x = 13 सेमी

परीक्षा: ज्यामिति- 1 - Question 6
Save

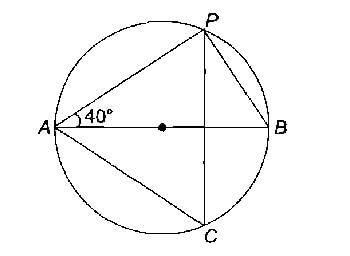
AB वृत्त का व्यास है और ∠PAB=40°
इस स्थिति में ∠PCA का मान क्या है?
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 6

समकोण त्रिकोण ΔPAB में

⇒ ∠PAB=40°          [ दिया गया ]

⇒ ∠BPA=90°       [ अर्धवृत्त में अंकित कोण ]

⇒ ∠PAB + ∠PBA + ∠BPA = 180°

∴   40° + ∠PBA + 90° = 180°

∴   ∠PBA = 180° - 130°

∴   ∠PBA = 50°

⇒   ∠PBA = ∠PCA = 50°      [ एक ही आर्क PA में अंकित कोण ]

∴   ∠PCA = 50°

परीक्षा: ज्यामिति- 1 - Question 7
Save

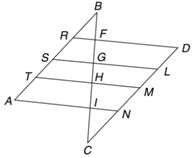
चित्र में, AB CD के समानांतर है और RD || SL || TM || AN है, और BR : RS : ST : TA = 3 : 5 : 2 : 7 है। यदि ज्ञात है कि CN = 1.333 BR है। BF : FG : GH : HI : IC का अनुपात ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 7

चूंकि AB और CD एक दूसरे के समानांतर हैं, और रेखाएँ RD और AN भी समानांतर हैं, इसका अर्थ है कि त्रिकोण RBF और NCI एक दूसरे के समान हैं। चूंकि CN : BR = 1.333 है, यदि हम BR को 3 मानते हैं, तो CN 4 होगा।

इसका अर्थ है कि BF : CI का अनुपात भी 3 : 4 होगा।
इसके अलावा, BR : RS : ST : TA = BF : FG : GH : HI = 3 : 5 : 2 : 7 (दिया गया)।

इसलिए, सही उत्तर है 3 : 5 : 2 : 7 : 4 

परीक्षा: ज्यामिति- 1 - Question 8
Save

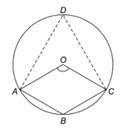
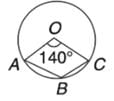
निम्नलिखित आकृति में, दिया गया है कि O वृत्त का केंद्र है और ∠AOC = 140° है। ∠ABC ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 8


∠AOC का छोटे क्षेत्र का = 140°
∠AOC का बड़े क्षेत्र का = 360° - 140° = 220°
सिद्धांत: केंद्र पर बना कोण वृत्त के परिधि पर बने कोण का दो गुना होता है।
इसलिए,


∴ ∠x का मान = 110°

परीक्षा: ज्यामिति- 1 - Question 9
Save

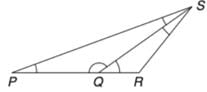
 नीचे दिए गए चित्र में, PQ = QS, QR = RS और कोण SRQ = 100° है। कोण QPS कितने डिग्री का है?
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 9

में ΔQRS, QR = RS
⇒ ㄥRQS = ㄥRSQ (क्योंकि समान भुजाओं के सामने वाले कोण समान होते हैं)।
इस प्रकार:

ㄥRQS + ㄥRSQ = 180° - 100° = 80°
ㄥRQS = ㄥRSQ = 40°
ㄥPQS = 180° – 40° = 140°  (एक रेखा पर कोणों का योग = 180°)

फिर, ㄥQPS = ㄥQSP (चूंकि समान भुजाओं के सामने वाले कोण समान होते हैं)

ㄥQPS + ㄥQSP = 180° – 140° = 40°
ㄥQPS = ㄥQSP = 20° 

परीक्षा: ज्यामिति- 1 - Question 10
Save

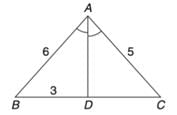
दी गई आकृति में, AD ∠BAC का द्विभाजक है, AB = 6 सेमी, AC = 5 सेमी और BD = 3 सेमी है। DC ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 10

परीक्षा: ज्यामिति- 1 - Question 11
Save

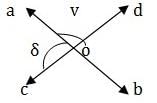
दी गई आकृति में, सीधी रेखाएँ AB और CD O पर मिलती हैं। यदि ∠δ = 3∠v है, तो ∠v = ?
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 11

COD एक सीधी रेखा है।
∴ ∠δ + ∠v = 180⁰ ⇒ 3v + v = 180 ⇒ 4v = 180 ⇒ v = 45⁰।

परीक्षा: ज्यामिति- 1 - Question 12
Save

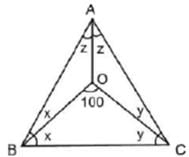
त्रिकोण ABC में, इनसेन्टर 0 पर है। यदि ㄥBOC = 100°, तो ㄥBAC ज्ञात करें।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 12

इन  ∠BOC

⇒ x + y = 80°

⇒ 2x + 2y = 160°

इसके अलावा, 2x + 2y + 2z = 180°

⇒ 160° + 2z = 180°

⇒ ∠BAC = 2z = 20°

परीक्षा: ज्यामिति- 1 - Question 13
Save

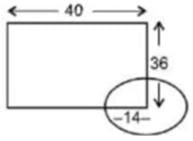
एक आयताकार बाड़ा 40 मीटर x 36 मीटर है जिसमें एक घोड़ा एक कोने पर 14 मीटर लंबी रस्सी से बंधा है। यदि घोड़ा बाड़े के बाहर है और यदि यह बाड़े के अंदर है, तो इसे घास काटने के लिए जो क्षेत्र मिल सकता है, उनका अनुपात क्या है?
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 13


  • एक आयत के कोने पर एक वृत्त की कल्पना करें।
  • वृत्त का 3 चौथाई हिस्सा आयत के बाहर और 1 चौथाई हिस्सा अंदर है।
  • इसलिए, आवश्यक अनुपात = 3 : 1
परीक्षा: ज्यामिति- 1 - Question 14
Save

नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का समाधान करें।
एक वर्ग का क्षेत्रफल एक आयत के क्षेत्रफल के बराबर है। इसके अलावा, वर्ग का परिमाण भी आयत के परिमाण के बराबर है।
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 14

यह संभव है केवल तब जब आयत की लंबाई और चौड़ाई दोनों वर्ग की भुजा के बराबर हों।

परीक्षा: ज्यामिति- 1 - Question 15
Save

एक चतुर्भुज एक वृत्त में अंकित है। यदि चारों खंडों के बाहर एक कोण अंकित है, तो इन चार कोणों का योग क्या है?
Detailed Solution for परीक्षा: ज्यामिति- 1 - Question 15

एक चतुर्भुज में अंकित चार कोणों का योग 360° है।

171 docs|185 tests
Join Course
Information about परीक्षा: ज्यामिति- 1 Page
In this test you can find the Exam questions for परीक्षा: ज्यामिति- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for परीक्षा: ज्यामिति- 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for परीक्षा: ज्यामिति- 1

Find all the important questions for परीक्षा: ज्यामिति- 1 at EduRev.Get fully prepared for परीक्षा: ज्यामिति- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the परीक्षा: ज्यामिति- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of परीक्षा: ज्यामिति- 1 resources.

परीक्षा: ज्यामिति- 1 MCQs with Answers

Prepare for the परीक्षा: ज्यामिति- 1 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for परीक्षा: ज्यामिति- 1 Quantitative Aptitude/संख्यात्मक योग्यता

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace परीक्षा: ज्यामिति- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup