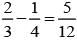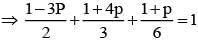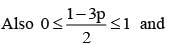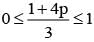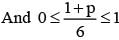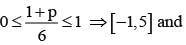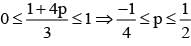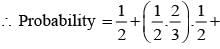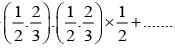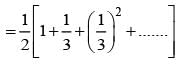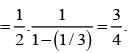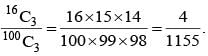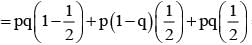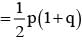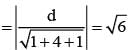JEE Advanced Level Test: Probability- 2 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Probability- 2
The equation of line of intersection of the planes x + 2y + z = 3 and 6x + 8y + 3z = 13 can be written as
The direction cosines of two lines are such that l + m + n = 0, l2 + m2 – n2 = 0, then angle between them is
The point of intersection of the lines 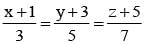 and
and 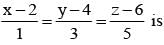
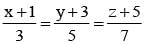 and
and 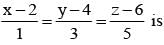
If the straight lines x = 1 + s, y = - 3 - λs, z = 1 + λs and x = t/2, y = 1 + t, z = -t + 2 with parameters s and t respectively are coplanar, then λ equals
If events are independent and P(A) = 1/3, P(B) = 1/3, P(C) = 1/4 then 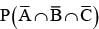 is equal to
is equal to
A fair die is tossed eight times. The probability that a third six is observed on the eight throw is
For k = 1, 2, 3, the box Bk contains k red balls and (k + 1) white balls. Let P(B1) = 1/2, P(B2) = 1/3, P(B3) = 1/6. A box is selected at random and a ball is drawn from it. If a red ball is drawn, then probability that it has come from box B2 is
Let A and B be two event such that 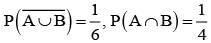
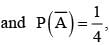 stands for complement of event A. Then events A and B are
stands for complement of event A. Then events A and B are
Three of the six vertices of a regular hexagon are chosen at random. The probability that triangle with three chosen vertices is an equilateral triangle is
If A and B are two events such that P(A∪B) = 3/4, P(A∩B) 1/4, 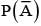 = 2/3, then
= 2/3, then 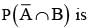
Three critics review a book. Odds in favour of book are 5 : 2, 4 : 3 and 3 : 4, respectively for the three critics. The probability that majority are in favour of the book is
Out of a set of integers given by {1, 2, 3, …. 30}, three numbers are selected at random. Find the probability the sum of the number chosen is divisible by 3.
A is a set containing n element. A subset P of A is chosen at random. The set A is reconstructed by replacing the element of P. A set ‘Q’ is again chosen at random. Find probability such that P∩Q = φ.
If the integers m and n are chosen at random from 1 to 100, then probability that a no. of form 7m + 7n is divisible by 5 equals
If 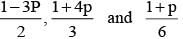 are the probability of three mutually exclusive and exhaustive events, then the set of all value of p is
are the probability of three mutually exclusive and exhaustive events, then the set of all value of p is
A man alternately tosses a coin and throws a dice beginning with the coin. The probability that he gets a head in the coin before he gets a 5 or 6 in the dice is
Three distinct numbers are selected from first 100 natural numbers. The probability that all the three numbers are divisible by 2 and 3 is
A student appears for test I, II and III. The student is successful if he passes either in test I and II or test I and III. The probability of the student passing in test I, II, III are p, q and 1/2 respectively. If the probability that the student is successful is 1/2, then
It is given that events A and B are such that P(A) = 1/4, P(A/B) = 1/2 and P(B/A) = 2/3, then P (B) is
Out of a set of integers given by {1, 2, 3, …. 30}, three numbers are selected at random. Find the probability the sum of the number chosen is divisible by 3.
The equation of plane passing through the point (0, 7, -7) and containing the line
The angle between line and plane 3x – 2y + 6z = 0 is (μ is scalar)
Let P(3, 2, 6) be a point in space and Q be a point on line Then value of m for which the vector
is parallel to the plane x-4y + 3z = 1 is
The equation of the plane through the point (-1, 2, 0) and parallel to the line 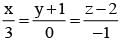 and
and 
Let A (1,1,1) , B (2, 3, 5) and C (-1, 0, 2) be three points, then equation of a plane parallel to the plane ABC which is at a distance 2 from origin is
The distance between the line and the plane
If the distance between the plane x - 2y + z = d and the plane containing the line 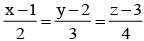 and
and 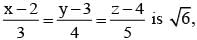 then |d| is
then |d| is
A plane π passes through the point (1, 1, 1). If b, c, a are the direction ratios of a normal to the plane, where a, b, c (a < b < c) are the prime factors of 2001, then the equation of the plane π is



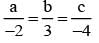
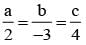
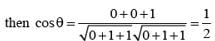

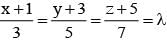
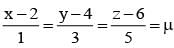
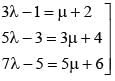 on solving λ = 1/2, & μ = -3/2
on solving λ = 1/2, & μ = -3/2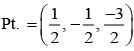
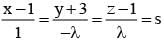
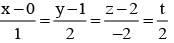
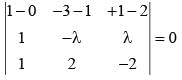
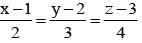 and
and 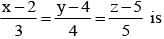
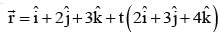
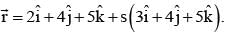
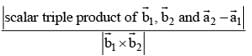
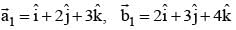
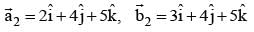
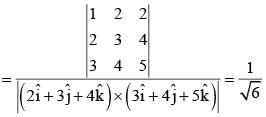
 = 1/3
= 1/3 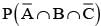 = 1/3, then
= 1/3, then 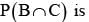
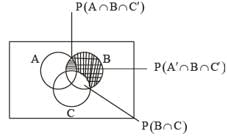
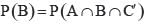

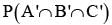
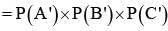
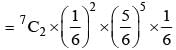
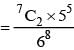
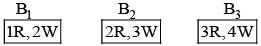
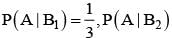

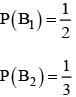
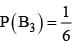
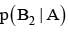
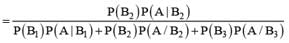
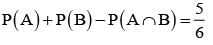
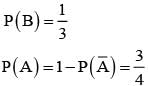
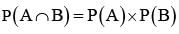
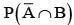 = P(B) - P(A∩B) =
= P(B) - P(A∩B) =