Test: Gravitation - 2 - Grade 12 MCQ
30 Questions MCQ Test - Test: Gravitation - 2
Four particles, each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction. (Take that gravitational force between two point masses m1 and m2 separated by is 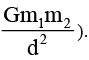 The speed of each particle is
The speed of each particle is
At what altitude will the acceleration due to gravity be 25% of that at the earth’s surface (given radius of earth is R)?
A planet of mass M is revolving around sun in an elliptical orbit. If dA is the area swept in a time dt, angular momentum can be expressed as
Let ω be the angular velocity of the earth’s rotation about its axis. Assume that the acceleration due to gravity on the earth’s surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth d below earth’s surface at a pole (d<<R) The value of d is
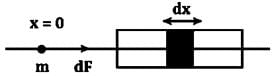
A straight rod of length L extends from x = a to x = L + a. Find the gravitational force exerted by it on a point mass m at x = 0 if the linear density of rod μ = A+ Bx2
With what angular velocity the earth should spin in order that a body lying at 30° latitude may become weightless [R is radius of earth and g is acceleration due to gravity on the surface of earth]
The work done in shifting a particle of mass m from centre of earth to the surface of earth is ( where R is the radius of the earth)
A man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface, he realizes that he will pass through a small hole in the planet. As he enters the hole, he sees that the planet is really made of two pieces a spherical shell of negligible thickness of mass 2M/3 and a point mass M/3 at the centre. Change in the force of gravity experienced by the man is
A particle is projected upward from the surface of earth (radius = R) with a speed equal to the orbital speed of a satellite near the earth’s surface. The height to which it would rise is
Two masses m1 & m2 are initially at rest and are separated by a very large distance. If the masses approach each other subsequently, due to gravitational attraction between them, their relative velocity of approach at a separation distance of d is :
The ratio of the energy required to raise a satellite to a height h above the earth to that of the kinetic energy of satellite in the orbit there is (R = radius of earth)
Two concentric shells of uniform density of mass M1 and M2 are situated as shown in the figure. The forces experienced by a particle of mass m when placed at positions A, B and C respectively are (given OA = p, OB = q and OC = r)
A spherical hole is made in a solid sphere of radius R. The mass of the original sphere was M.The gravitational field at the centre of the hole due to the remaining mass is
At what height above the earth’s surface does the acceleration due to gravity fall to 1% of its value at the earth’s surface?
A ring has a total mass m but not uniformly distributed over its circumference. The radius of the ring is R. A point mass m is placed at the centre of the ring. Work done in taking away the point mass from centre to infinity is
If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g the same?
Imagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force of attraction between the planet and the star is R−5/2 , then T2 is proportional to
Two point masses of mass 4m and m respectively separated by d distance are revolving under mutual force of attraction. Ratio of their kinetic energies will be :
If G is the universal gravitational constant and ρ is the uniform density of spherical planet.
Then shortest possible period of the planet can be
Four similar particles of mass m are orbiting in a circle of radius r is the same direction and same speed because of their mutual gravitational attractive force as shown in the figure. Speed of a particle is given by
A planet is moving in an elliptical path around the sun as shown in figure. Speed of planet in positional P and Q are υ1 and υ2 respectively with SP = r1 and SQ = r2 , then υ1/υ2 is equal to
Consider two configurations of a system of three particles of masses m, 2m and 3m. The work done by external agent in changing the configuration of the system from figure (i) to figure (ii) is
Three solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any sphere at the time of collision would be
Three particles P, Q and R placed as per given figure. Masses of P, Q and R are √3 m, √3 m and m respectively. The gravitational force on a fourth particle ‘S’ of mass m is equal to
How much deep inside the earth should a man go so that his weight becomes one fourth of that at a point which is at a height R above the surface of earth .
Three identical stars of mass M are located at the vertices of an equilateral triangle with slide L. The speed at which they will move if they all revolve under the influence of one another’s gravitational force in a circular orbit circumscribing the triangle while still preserving the equilateral triangle
The period of revolution of planet A around the sun is 8 times that of B. The distance of A from the sun is x times that of B from the sun. Find x.
n – particles each of mass m0 are placed on different corners of a regular polygon of edge length a. The distance between vertex and centre of polygon is r0 . The gravitational potential at the centre of the polygon is
If an artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of the escape velocity form the earth, the height of the satellite above the surface of the earth is
A uniform ring of mass M and radius R is placed directly above uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d = √3R from the centre of sphere. The gravitational attraction between the sphere and the ring is



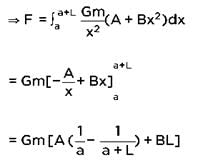
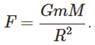
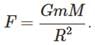

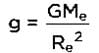
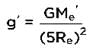
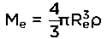
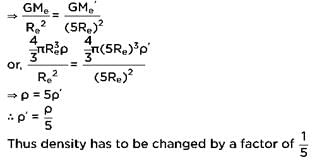

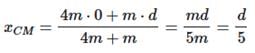

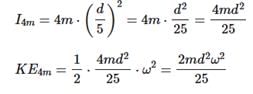
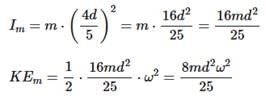

 and ATQ TA = 8TB so,
and ATQ TA = 8TB so,










