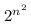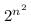Test: Introduction To Relations - JEE MCQ
20 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Introduction To Relations
Let R = {(P, Q) : OP = OQ , O being the origin} be an equivalence relation on A. The equivalence class [(1, 2)] is
Let a relation T on the set R of real numbers be T = {(a, b) : 1 + ab < 0, a, ∈ R}. Then from among the ordered pairs (1, 1), (1, 2), (1, -2), (2, 2), the only pair that belongs to T is________.
For real number x and y, we write xRy ⇔ x-y + √2 is an irrational number. Then the relation R is:
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relation on the set A = {1, 2, 3, 4}. The relation R is
If A = {1, 3, 5, 7} and we define a relation R = {(a, b), a, b ∈ A: |a - b| = 8}. Then the number of elements in the relation R is
If A = {1, 3, 5, 7} and define a relation, such that R = {(a, b) a, b ∈ A : |a + b| = 8}. Then how many elements are there in the relation R
In the set N x N, the relation R is defined by (a, b) R (c, d) ⇔ a + d = b + c. Then R is
If A = {1, 2, 3, 4} and B = {1, 3, 5} and R is a relation from A to B defined by(a, b) ∈ element of R ⇔ a < b. Then, R = ?
Let R be the relation on the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3,3), (3,2)}. then R is
Let A = {1, 2, 3, 4, 5, 6, 7}. P = {1, 2}, Q = {3, 7}. Write the elements of the set R so that P, Q and R form a partition that results in equivalence relation.
Let R be a relation on set A of triangles in a plane.
R = {(T1, T2) : T1, T2 element of A and T1 is congruent to T2} Then the relation R is______
Which one of the following relations on set of real numbers is an equivalence relation?
Let C = {(a, b): a2 + b2 = 1; a, b ∈ R} a relation on R, set of real numbers. Then C is
Let A = {1, 2, 3, 4} and B = {x, y, z}. Then R = {(1, x), (2, z), (1, y), (3, x)} is
Let R be a relation on N, set of natural numbers such that m R n ⇔ m divides n. Then R is
If R be a relation “less than” from set A = {1, 2, 3, 4} to B = {1, 3, 5}, i.e. (a, b) ∈ R if a < b, if (b, a) ∈ R-1elements in R-1 are
Let R be a relation on a finite set A having n elements. Then, the number of relations on A is
Let R be a relation on N (set of natural numbers) such that (m, n) R (p, q) mq(n + p) = np(m + q). Then, R is
A situation in which significant power is distributed among three or more states is known as what?
Let R be an equivalence relation on Z, the set of integers.
R = {(a, b): a,b ∈ Z and a – b is a multiple of 3} The Equivalence class of [1] is
|
204 videos|290 docs|139 tests
|