Test: Introduction To Vector Algebra - JEE MCQ
20 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Introduction To Vector Algebra
For what values of x and y, the vectors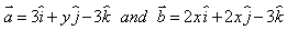 are equal?
are equal?
Two or more vectors having the same initial point are called
If the magnitude of the position vector is 7, the value of x is:
If 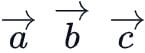 and
and 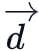 are the position vectors of the points A, B, C and D such that
are the position vectors of the points A, B, C and D such that 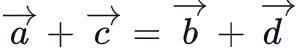 then ABCD is:
then ABCD is:
The angles α, β, γ made by the vector with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
are:
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be
If and
, then the value of scalars x and y are:
The unit vector in the direction of , where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:
A vector of magnitude 14 units, which is parallel to the vector
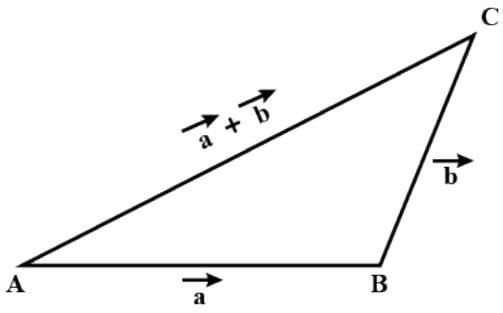
For any two vectors a and b, we always have
If l, m, n are the direction cosines of a position vector  then which of the following is true?
then which of the following is true?
A vector whose initial and terminal points coincide, is called
A point from a vector starts is called______and where it ends is called its______.
If are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are collinear.
|
204 videos|290 docs|139 tests
|



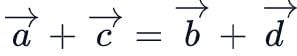

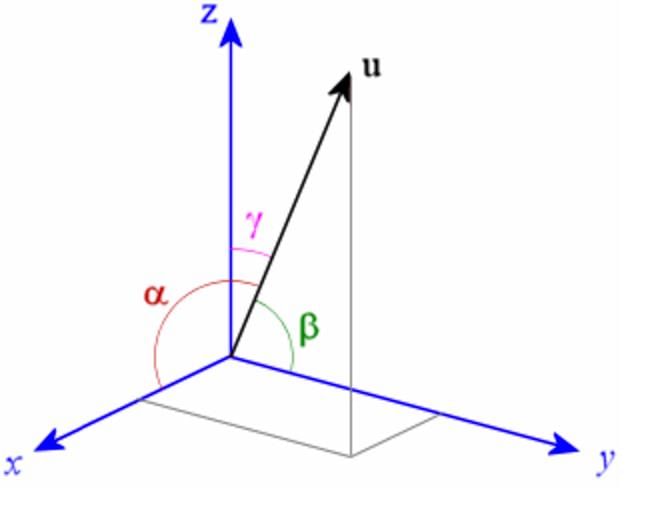
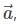 is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector
is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector 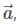 with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector
with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector 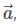 denoted by l, m, n, then
denoted by l, m, n, then
















