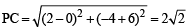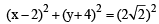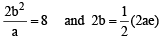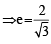Test: JEE Main 35 Year PYQs- Conic Sections - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - Test: JEE Main 35 Year PYQs- Conic Sections
Two common tangents to the circle x2 + y2 = 2a2 and parabola y2 = 8ax are [2002]
The normal at the point (bt12 , 2bt1) on a parabola meets the parabola again in the point (bt22, 2bt2) , then [2003]
The foci of the ellipse 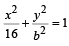 and the hyper bola
and the hyper bola 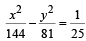 coincide. Then the value of b2 is [2003]
coincide. Then the value of b2 is [2003]
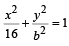 and the hyper bola
and the hyper bola 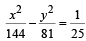 coincide. Then the value of b2 is [2003]
coincide. Then the value of b2 is [2003]If a ≠ 0 an d the lin e 2bx + 3cy + 4d=0 passes through the points of intersection of the parabolas y2 = 4ax and x2 = 4ay, th en [2004]
The eccentricity of an ellipse, with its centre at the origin, is.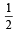 If one of the directrices is x = 4 , then the equation ofthe ellipse is: [2004]
If one of the directrices is x = 4 , then the equation ofthe ellipse is: [2004]
Let P be the point ( 1, 0 ) and Q a point on the locus y2 = 8x .The locus of mid point of PQ is [2005]
The locus of a point P (α, β) moving under the condition th at the line y = αx + β is a tangen t to the hyper bola 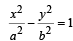 is [2005]
is [2005]
An ellipse has OB as semi minor axis, F and F ' its focii and the angle FBF ' is a right angle. Then the eccentricity of the ellipse is [2005]
The locus of the vertices of the family of parabol as 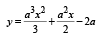 [2006]
[2006]
In an ellipse, the distance between its foci is 6 and minor axis is 8. Then its eccentricity is [2006]
Angle between the tangents to the curve y = x2 - 5x+6 at the points (2, 0) and (3, 0) is [2006]
For the Hyper bola 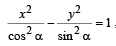 which of the following remains constant when a varies = ? [2007]
which of the following remains constant when a varies = ? [2007]
The equation of a tangent to the parabola y2 = 8x is y = x + 2. The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is [2007]
The normal to a curve at P(x, y) meets the x-axis at G. If the distance of G from the origin is twice the abscissa of P, then the curve is a [2007]
A focus of an ellipse is at the origin. The directrix is the line x = 4 and the eccentricity is 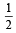 . Then the length of the semi-major axis is [2008]
. Then the length of the semi-major axis is [2008]
A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at [2008]
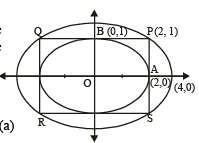
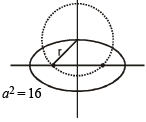
The ellipse x2 + 4y2 = 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is : [2009]
If two tangents drawn from a point P to the parabola y2 = 4x are at right angles, then the locus of P is [2010]
Equation of the ellipse wh ose axes ar e th e axes of coordinates and which passes through the point (–3, 1) and has eccentricity 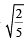 is [2011]
is [2011]
Statement-1 : An equation of a common tangent to the parabola y2 = 16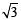 x and the ellipse 2x2 + y2 =4 is y = 2x+ 2
x and the ellipse 2x2 + y2 =4 is y = 2x+ 2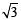
Statement-2 : If the line 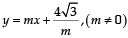 is a common tan gent to the parabola y2 = 16
is a common tan gent to the parabola y2 = 16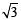 x and the ellipse 2x2 + y2 = 4, then m satisfies m4 + 2m2 = 24 [2012] [2012]
x and the ellipse 2x2 + y2 = 4, then m satisfies m4 + 2m2 = 24 [2012] [2012]
An ellipse is drawn by taking a diameter of the circle (x – 1)2 + y2 = 1 as its semi-minor axis and a diameter of the circle x2 + (y – 2)2 = 4 is semi-major axis. If the centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is : [2012]
The equation of the circle passing through the foci of the ellipse 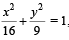 and having centre at (0, 3) is [JEE M 2013]
and having centre at (0, 3) is [JEE M 2013]
Given : A circle, 2x2 + 2y2 = 5 and a parabola, 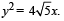
Statement-1 : An equation of a common tangent to these curves is 
Statement-2 : If the line, 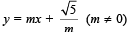 is theircommon tangent, then m satisfies m4 – 3m2 + 2 = 0. [JEE M 2013]
is theircommon tangent, then m satisfies m4 – 3m2 + 2 = 0. [JEE M 2013]
The locus of the foot of perpendicular drawn from the centre of the ellipse x2 + 3y2 = 6 on any tangent to it is [JEE M 2014]
The slope of the line touching both the parabolas y2 = 4x and x2 =-32y is [JEE M 2014]
Let O be the vertex and Q be any point on the parabola, x2 = 8y. If the point P divides the line segment OQ internally in the ratio 1 : 3, then locus of P is : [JEE M 2015]
The normal to the curve, x2 + 2xy – 3y2 = 0, at (1, 1) [JEE M 2015]
The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latera recta to the ellipse 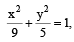 is : [JEE M 2015]
is : [JEE M 2015]
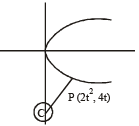
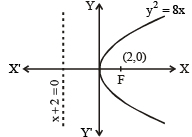
Let P be the point on the parabola, y2 = 8x which is at a minimum distance from the centre C of the circle, x2 + (y + 6)2 = 1.Then the equation of the circle, passing through C and having its centre at P is: [JEE M 2016]
The eccentricity of the hyperbola whose length of the latus rectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is : [JEE M 2016]
|
149 videos|192 docs|197 tests
|


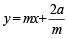 ...(i)
...(i)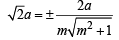

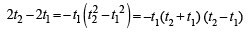
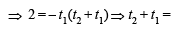
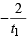

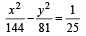
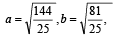
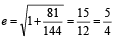
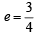

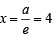
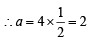
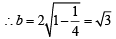
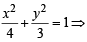 3x2 + 4y2 = 12
3x2 + 4y2 = 12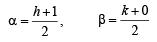
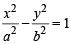 is
is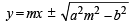
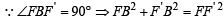
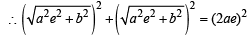
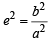
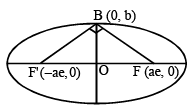
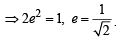
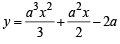
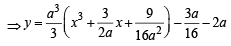
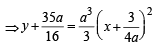
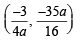
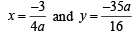

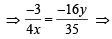 64xy = 105
64xy = 105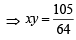 which is the required locus.
which is the required locus.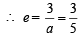
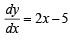 ∴ m1 = (2x - 5)(2, 0) =-1 ,
∴ m1 = (2x - 5)(2, 0) =-1 ,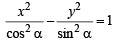
 Here, a2 = cos2α and b2 = sin2α
Here, a2 = cos2α and b2 = sin2α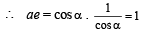
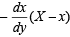
 ⇒
⇒ 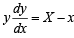
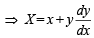 ∴ Co-ordinate of G
∴ Co-ordinate of G 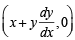
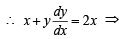
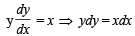
 ⇒ x2 – y2 = –2c1
⇒ x2 – y2 = –2c1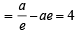
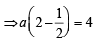
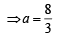

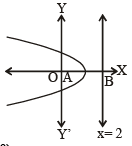
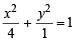
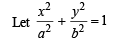
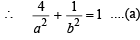
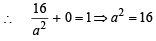
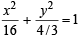 or x2 + 12y2 =16
or x2 + 12y2 =16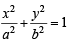
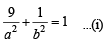
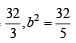
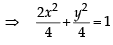
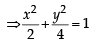
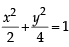
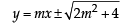 ...(1)
...(1)
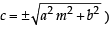
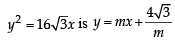 ...(2)
...(2)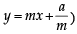
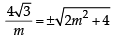
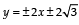
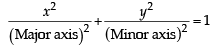
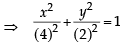

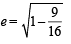
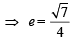
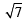 , 0)
, 0)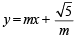
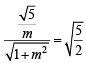
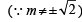
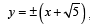 both statements are correct as m = ±1 satisfies the given equation of statement-2.
both statements are correct as m = ±1 satisfies the given equation of statement-2.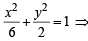 a2 = 6, b2 = 2
a2 = 6, b2 = 2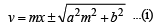
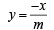 ...(ii)
...(ii)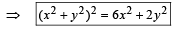
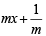
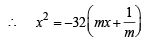
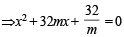
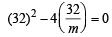
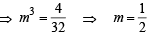
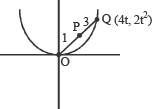
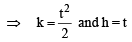
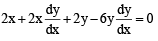
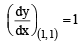
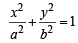 in first quadrant is
in first quadrant is 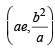 and the tangent at this point intersects x-axis at
and the tangent at this point intersects x-axis at 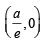 and y-axis at (0, a).
and y-axis at (0, a).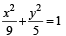
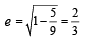
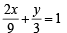
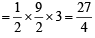
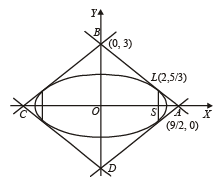
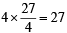 sq. units.
sq. units.