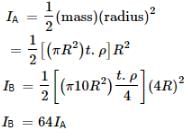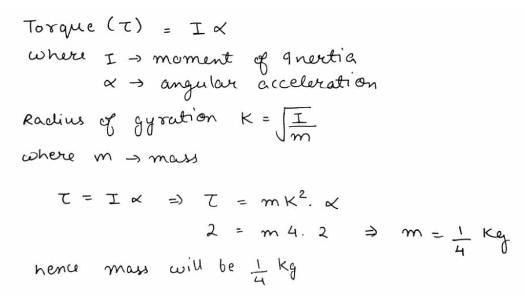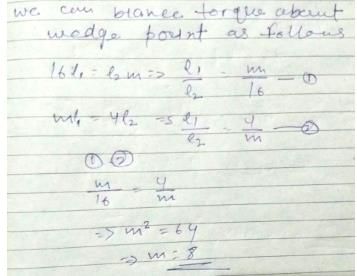Test: Rotational Motion - NEET MCQ
30 Questions MCQ Test Physics Class 11 - Test: Rotational Motion
Two spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be -
A disc of metal is melted to recast in the form of a solid sphere. The moment of inertias about a vertical axis passing through the centre would -
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is
A stone of mass 4kg is whirled in a horizontal circle of radius 1m and makes 2 rev/sec. The moment of inertia of the stone about the axis of rotation is
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
For the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body
Moment of inertia of a thin semicircular disc (mass = M & radius = R) about an axis through point O and perpendicular to plane of disc, is given by :
A rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of inertia is given by
I = 2x2 - 12x + 27 The x-coordinate of centre of mass is
Consider the following statements
Assertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.
Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :
A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
One end of a uniform rod of mass m and length I is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity w. The force exerted by the clamp on the rod has a horizontal component
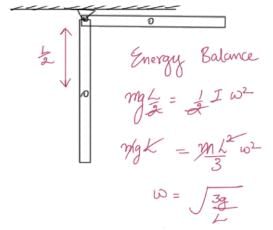
A rod of length 'L' is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod when it is in vertical position is
A disc of radius 2m and mass 200kg is acted upon by a torque 100N-m. Its angular acceleration would be
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.
A torque of 2 newton-m produces an angular acceleration of 2 rad/sec2 a body. If its radius of gyration is 2m, its mass will be:
A particle is at a distance r from the axis of rotation. A given torque t produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is
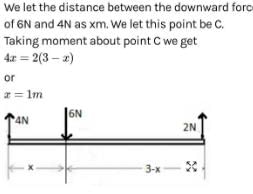
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is :
In an experiment with a beam balance on unknown mass m is balanced by two known mass m is balanced by two known masses of 16 kg and 4 kg as shown in figure.
The value of the unknown mass m is
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is :
Consider the following statements
Assertion (A) : A cyclist always bends inwards while negotiating a curve
Reason (R) : By bending he lowers his centre of gravity Of these statements,
|
97 videos|379 docs|103 tests
|