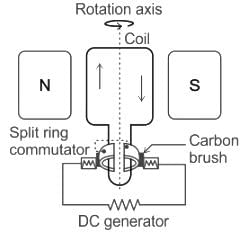
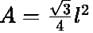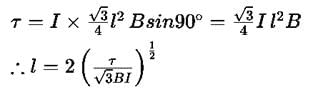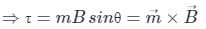Test: Torque on Current Carrying Loop - NEET MCQ
10 Questions MCQ Test Topic-wise MCQ Tests for NEET - Test: Torque on Current Carrying Loop
A conductor of length l, carrying current I and placed in a magnetic field B experiences a force F given by
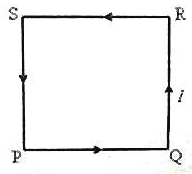
A plane square loop PQRS of side ‘a’ made of thin copper wire has ‘n’ turns and it carries a direct current ‘I’ ampere in the direction shown in the adjoining figure. This wire loop is placed in a magnetic field of flux density ‘B’ tesla, which is directed perpendicularly in to the plane of the loop. What is the torque acting on the loop?
A rectangular current-carrying coil of length 2 m and width 4 m, having 100 turns, is placed in a uniform magnetic field of 0.05 tesla. If the angle between the area vector of the coil and the magnetic field is 90°, and the current in the coil is 3 A, find the torque acting on the coil due to the magnetic field.
A wire of length l, carrying current is bent into a loop and placed with its plane perpendicular to a magnetic field. In which of the following shapes, is the torque acting on the loop maximum?
A circular coil of radius 0.50 m and 100 turns, carrying a current of 80 mA, is placed such that the normal to its plane makes an angle of 30° with a uniform magnetic field of 4.0 T. The magnitude of torque acting on the coil is:
A current loop of area 0.01m2 and carrying a current of 100 A is held parallel to a magnetic field of intensity 0.1 tesla. The torque in Nm acting on the loop is:
A circular loop is placed in an external magnetic field. How is the torque 'τ' related to radius 'r' of the loop?
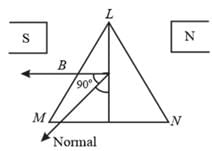
A coil in the shape of an equilateral triangle of side l, is suspended between two pole pieces of a permanent magnet such that magnetic field B is in the plane of the coil. If due to current I in the triangle, a torque τ acts on it. The side l of the triangle is
A rectangular loop of N number of turns encloses an area A. If the current I flows in the loop, then the magnetic moment of the loop will be:
A current carrying coil having magnetic moment M is placed in a magnetic field B. Initially the magnetic field is perpendicular to the plane of the coil and then coil turned about an axis such that the angle between the magnetic field and the plane of the coil become zero. Then choose the correct statement.
|
9 docs|826 tests
|