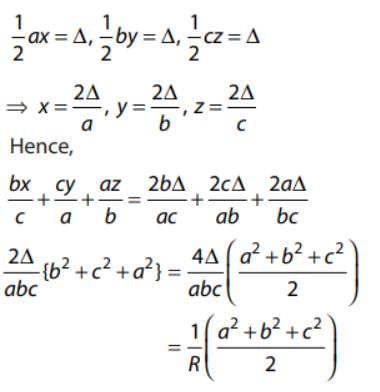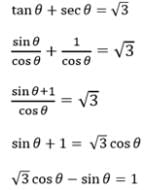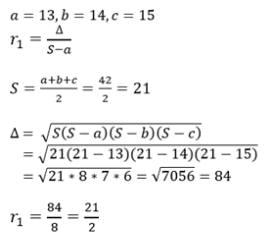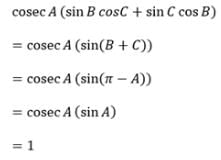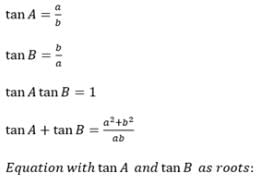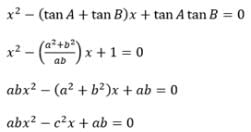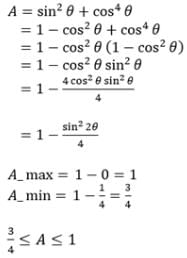Test: Trigonometric Functions - 2 - Commerce MCQ
25 Questions MCQ Test Online MCQ Tests for Commerce - Test: Trigonometric Functions - 2
Angles of triangle are in A.P. If the number of degrees in the smallest to the number of radians in the largest is as 60:π, then the smallest angle is
If x, y, z are perpendiculars drawn from the vertices of a triangle having sides a, b and c, then bx/c + cy/a + az/b =
If tan θ + sec θ = √3, 0 < π , then θ is equal to
If sin (120°−α) = sin(120°−β) and 0 <α,β<π, then all values of α and β are given by
The equation (cos π – 1) x2 + cos π) x + sin π = 0, where x is a variable, has real roots. Then the interval of π may be any one of the following:
In a triangle ABC, a = 13, b = 14, c = 15, then r1 =
In a triangle ABC, cosec A (sin B cos C + cos B sin C) equals
If the angles of at triangle are in the ratio 1 : 2 : 3, then the sides are in the ratio
In a triangle ABC right angled at C, tan A and tan B satisfy the equation
Let the angles A, B, C of ΔABC be in A.P. and let b: c:: √3 : √2, then the angle A is
If A = sin2θ+cos4θ then for all real values of θ
If the radius of the circumcircle of an isosceles triangle PQR is equal to PQ (= PR), then the angle P is
The maximum value of sin 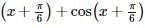 in the interval
in the interval 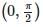 is attained at
is attained at
The general solution of the equation sin x + cos x = 2 is
If x = y cos 2π/3 = z cos 4π/3, then xy + yz +zx
|
705 tests
|