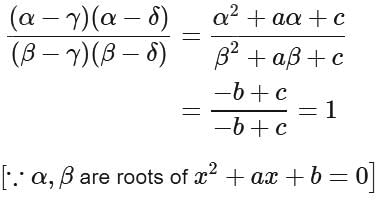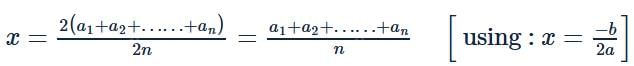Test: Quadratic Equations - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Quadratic Equations
Find the positive value of k for which the equations : x2 + kx + 64 = 0 and x2 – 8x + k = 0 will have real roots:
Find the condition that one root is double the of ax2 + bx + c = 0
If the roots of the equation x2 – 15x2 + kx – 45 = 0 are in A.P., find value of k:
If the roots of the equation kx2 – 3x -1= 0 are the reciprocal of the roots of the equation x2 + 3x – 4 = 0 then K =
The value of p and q(p ≠ 0,q ≠ 0) for which p, q are the roots of the equation x2 + px + q = 0 are
If difference between the roots ofthe equation x2 – kx + 8 = 0 is 4 then the value of K is:
If the roots of the equation 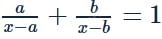 are equal in magnitude and opposite in sign, then
are equal in magnitude and opposite in sign, then
Suppose a,b,c ∈ R and b ≠ c. If α, β are roots of x2 + ax + b = 0 and γ, δ are roots of x2 + ax + c = 0, then value of 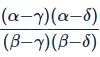 is independent of:
is independent of:
If a ∈ R and a1, a2, a3……,an ∈ R then (x − a1)2 + (x − a2)2 +…+ (x − an)2 assumes its least value at x=
Numbers of values of k for which roots of equation x2 − 3x + k = 0 lie in the interval (0,1) is
|
209 videos|447 docs|187 tests
|
|
209 videos|447 docs|187 tests
|