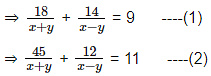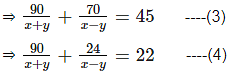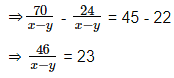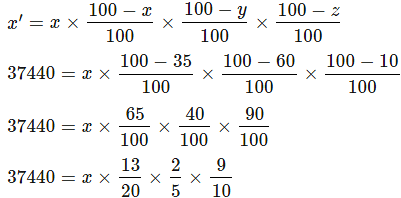SSC CGL (Tier II) Practice Test - 1 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier II Mock Test Series 2024 - SSC CGL (Tier II) Practice Test - 1
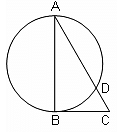
Suppose AB is the diameter of the circle as shown, BC is tangent to the circle, ∠BAC = 30° and CD = √3. What is the distance between A and B?

Which of the following statement(s) is/are TRUE?
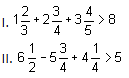
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a set of three numbers, the average of first two numbers is 21, the average of the last two numbers is 24, and the average of the first and the last numbers is 15. What is the average of the three numbers?
Three dice are rolled together. What is the probability of getting the same number on the three?
A, B and C can build a wall in 12 days together. C is four times as productive as B and A alone can build the wall in 48 days. In how many days can A and B working together build the wall?
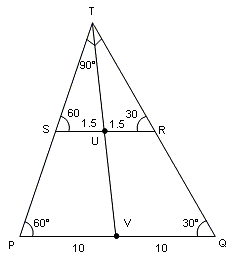
In a trapezium PQRS, PQ is parallel to RS, PQ = 20 cm, RS = 3 cm, ∠PQR = 30° and ∠QPS = 60°. What is the length of the line joining the midpoints of PQ and RS?
If the angles A, B and C of a triangle are in the ratio 2 : 3 : 7, then the sides a, b and c will be in the ratio
A bank gives Rs. 25,000 on saving a certain principal in 2 years at 8% rate of interest. How much will the bank give (in Rs.) on the same principal in 4 years at the same rate of interest compounded annually?
Directions: Study the information carefully to answer the question that follows.
Number of students that appeared in MBA entrance exam from 2008-2011 = 8,00,000
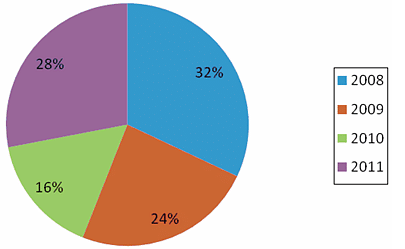
Percentage breakup of number of students that appeared for MBA entrance exam in 2008:
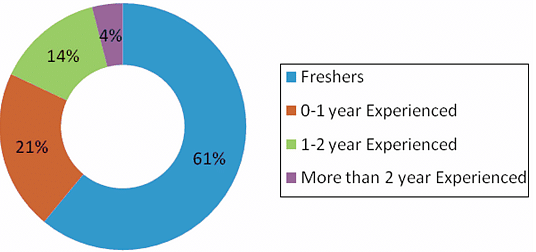
(Note: 0-1 year experienced means the person is having work experience greater than 0 years and up to 1 year.)
Q. The students who appeared for MBA entrance exam in 2008 having more than 2 years of experience, were what percent less than the students who appeared for MBA exam in 2011?
Two dice are thrown. Find the probability that the product of two numbers received is even.
If (1/21) + (1/22) + (1/23) ... + (1/210) = 1/k, then what is the value of k?
Directions: Study the information carefully to answer the question that follows.
Number of students that appeared in MBA entrance exam from 2008-2011 = 8,00,000
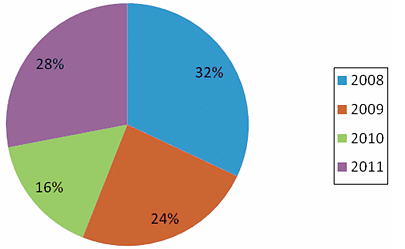
Percentage breakup of number of students that appeared for MBA entrance exam in 2008:
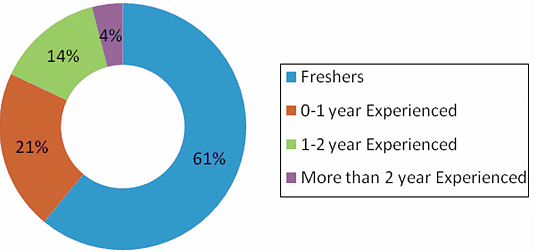
(Note: 0-1 year experienced means the person is having work experience greater than 0 years and up to 1 year.)
Q. If the MBA entrance test fees increased by 15% from 2008 to 2009, what was the percent change in the total fees paid by the students in 2009 to that in 2008?
Directions: Study the information carefully to answer the question that follows.
Number of students that appeared in MBA entrance exam from 2008-2011 = 8,00,000
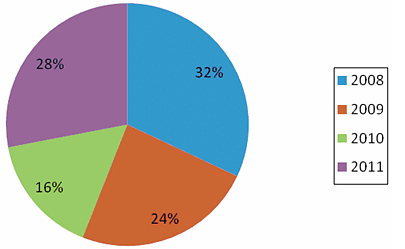
Percentage breakup of number of students that appeared for MBA entrance exam in 2008:

(Note: 0-1 year experienced means the person is having work experience greater than 0 years and up to 1 year.)
Q. If, out of the total number of students that appeared for MBA entrance exam during 2009-2011, exactly 41% were 0-1 year experienced. Find the total number of students that appeared for MBA entrance exam during 2008-2011, who were having 0-1 year experience.
A certain sum of money amounts to $1600 in 4 years and further to $1800 in 6 years at simple interest. How much will it amount to in 10 years?
If ![]() and a sinθ - b cosθ = 0 then find the value of a2 + b2. (If sinθ, cosθ ≠ 0)
and a sinθ - b cosθ = 0 then find the value of a2 + b2. (If sinθ, cosθ ≠ 0)
If the greatest number of six digit 435a1b is divisible by 45 then find the value of 101a + 99b.
A boat covers a distance of 18 km downstream and 14 km upstream in 9 hours and It covers a distance of 45 km downstream and 12 km upstream in 11 hours. What is the speed (in km/hr) of the current?
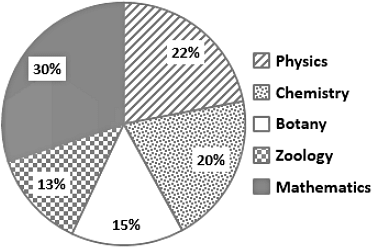
Study the given pie - chart and table carefully and answer the question that follows. The percentage wise distribution of lecturers in five different subjects in a university is shown in the pie chart.
The total number of lecturers is 500.
Ratio of male to female lecturers:
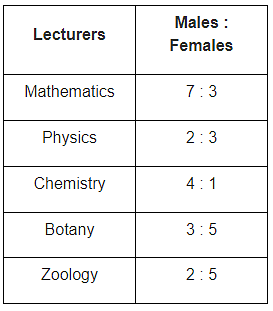
Q. What is the difference in the number of female lecturers in chemistry and Mathematics?
Rs. 30000 is borrowed at compound interest at the rate of 8 percent per annum. If the interest is compounded quarterly, then how much amount will have to be paid after 6 months?
A student obtained equal marks in english and history. The ratio of marks in history and maths is 3 ∶ 4. He scored an aggregate of 60 percent in the three subjects. Maximum marks for each subject is 100. How much did he score in history?
If Sarita had walked at a speed of 15 km/h instead of 10 km/h, she would have walked 40 km more in the same time. What is the actual distance travelled by her?
A man sold a car at 12 percent profit and a bike at 12 percent profit. If he had sold the car at 21 percent profit and the bike at 12 percent profit, then he would have gained Rs. 4500 more. If the total cost price of car and bike is Rs. 75000, then what is the respective cost price of bike and car?
When a number is successively decreased by 35 percent, 60 percent and 10 percent, then it becomes 37440. What is that number?
A borewell with a diameter of 20 m from the inside is dug 10 m deep. Soil taken out of it has been evenly spread all around it to a width of 30 m to form an embankment. Find the height (in m) of the embankment.
Mean of twenty observations is 15. If two observations 3 and 14 are replaced by 8 and 9 respectively, then the new mean will be:
Study the following table carefully and answer the question given below it:
Number of candidates appearing for an interview for a post in various Banks and percentage of candidates qualifying.
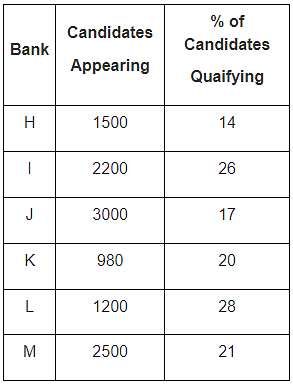
Q. The number of candidates who did not qualify in bank K was approximately what percent of the candidates who did not qualify in bank I ?
The ratio of the salaries of Akhshay and Amir is 8 ∶ 9. If Akhshay’s salary is increased by 50% and Amir’s salary is reduced by 25%, then their ratio becomes 16 ∶ 9. What is the salary of Akshay?
The cost of 2 sarees and 4 shirts is Rs 16,000 while the cost of 1 saree is equal to the cost of 6 shirts. The cost of 12 shirts is:
If a +1/b = 1 and b +1/c = 1, then c +1/a is equal to:
|
66 docs|139 tests
|
|
66 docs|139 tests
|


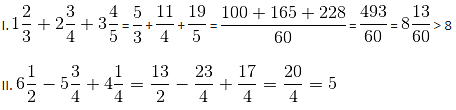
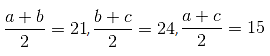
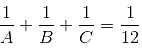 --- (i)
--- (i)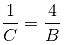
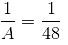
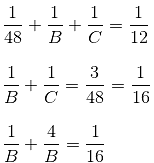
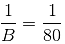

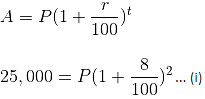 ... (i)
... (i)