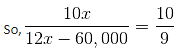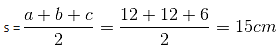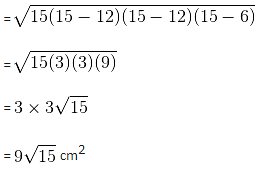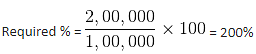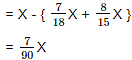SSC CGL (Tier II) Practice Test - 10 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier II Mock Test Series 2024 - SSC CGL (Tier II) Practice Test - 10
How many two-digit prime numbers are there between 10 and 100 which remain prime numbers when the order of their digits is reversed?
A taxi goes from City A to City B at an average speed of 84 km/hr. In the return journey, due to traffic the average speed of the taxi falls by 24 km/hr. Find the average speed of the taxi (in km/hr) for the total journey.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Five friends purchased some books from a book shop. Four of them purchased books worth $30 each. If the fifth one purchased books worth $40 more than the average of all of them together, what was the total cost of the books purchased by all?
A grain trader has 100 bags of rice. He sold some bags at 10% profit and rest at 20% profit. His overall profit on selling these 100 bags was 14%. How many bags did he sell at 20% profit?
Two dice are thrown at the same time and the product of numbers appearing on them is noted. The probability that the product is less than 9 will be
The ratio of the bank balances of three brothers A, B and C is 10 : 12 : 5, respectively. B transfers Rs. 60,000 from his account to C's. The new ratio of the bank balances becomes 10 : 9 : 8. What is the bank balance of A (in Rs.)?
If 3x + 6y + 9z = 20/3 , 6x + 9y + 3z = 17/3 and 18x + 27y - z = 11/9 , then what is the value of 75x + 113y?
A water tap fills a tub in 'p' hours and a sink at the bottom empties it in 'q' hours. If p < q and both tap and sink are open, the tank is filled in 'r' hours; then
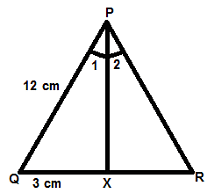
In a triangle PQR, PX bisects QR. PX is the angle bisector of angle P. If PQ = 12 cm and QX = 3 cm, then what is the area (in cm2) of triangle PQR?
The arithmetic mean of the following numbers 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6 and 7, 7, 7, 7, 7, 7, 7 is
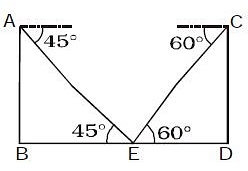
Two trees are standing along the opposite sides of a road. The distance between the two trees is 400 metres. There is a point on the road between the trees. The angles of depression of the point from the top of the trees are 45° and 60°. If the height of the tree which makes 45° angle is 200 metres, then what will be the height (in metres) of the other tree?
Directions: Study the following information to answer the question.
The table given below shows the ratio of cars and bikes manufactured by five different companies. The table also shows the ratios of three different types of cars C1, C2 and C3 and three different types of bikes B1, B2 and B3 manufactured by these five different companies. The total numbers of cars and bikes together manufactured by D, E, F, G and H are 3,00,000, 2,80,000, 3,20,000, 4,00,000 and 4,80,000, respectively.
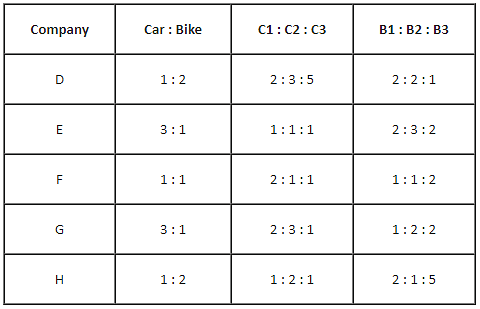
Total number of bikes manufactured by company D is what percentage of the total number of cars of type C1 manufacture by company G?
Directions: Study the following information to answer the question.
The table given below shows the ratio of cars and bikes manufactured by five different companies. The table also shows the ratios of three different types of cars C1, C2 and C3 and three different types of bikes B1, B2 and B3 manufactured by these five different companies. The total numbers of cars and bikes together manufactured by D, E, F, G and H are 3,00,000, 2,80,000, 3,20,000, 4,00,000 and 4,80,000, respectively.
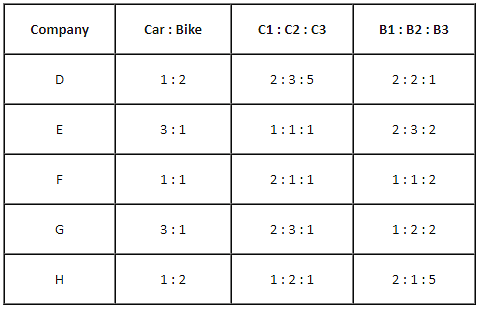
What is the difference between the total number of cars of type C3 manufactured by companies E and G together and the number of bikes of type B1 manufactured by company H?
Directions: Study the following information to answer the question.
The table given below shows the ratio of cars and bikes manufactured by five different companies. The table also shows the ratios of three different types of cars C1, C2 and C3 and three different types of bikes B1, B2 and B3 manufactured by these five different companies. The total numbers of cars and bikes together manufactured by D, E, F, G and H are 3,00,000, 2,80,000, 3,20,000, 4,00,000 and 4,80,000, respectively.

A = Total number of cars manufactured by all the companies
K = Difference between the number of C3 type cars manufactured by company H and the number of B3 type bike manufactured by company E
What is the value of A : K?
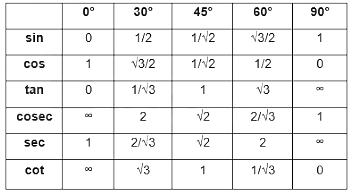
Find the value of sin4 30° + cos4 30° - sin 25° cos 65° - sin 65° cos25°.
A is driving a car along the highway at a speed of 90 km/hr. B, driving a car at a constant speed on the same highway and in the same direction, crossed it. After 12 seconds, B has crossed A, and the distance between their cars is 100 meters. The speed (in km/h) of B's car is:
A thief is chased by police and caught. The thief was 40 m ahead of the police and the speeds of the thief and the police are 10 m/s and 15 m/s, respectively. Find the total distance travelled by police.
A can do a piece of work in 82 days, B can do in 123 days and C can do the same work alone in 164 days. If on the first day A worked alone and on the second day B and C worked together and on the third day A and C worked together. If they repeat the cycle, then in how many days total work can be completed?
A milkman has two types of milk of equal quantity. He sells one at Rs.61/ltr. and other at Rs.57/ltr. After selling ½ of both the milk i.e. 33ltrs of each type of milk he experienced loss of 60%. Now he mix both type of milk and sell the mixture at Rs.P/ltr. Find the value of P if he wishes to cover all his losses.
The expenditures (in thousands) of two companies (A and B) on various heads in a given year are provided in the following bar graph.
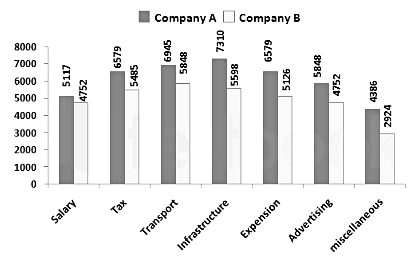
Q. The expenditure made by both companies together on salary was approximately what percentage of their expenses on Infrastructure?
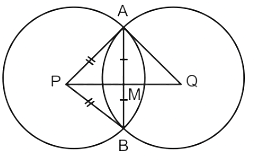
Two circles of radius 13 cm and 15 cm intersect each other at points A and B. If the length of the common chord is 24 cm, then what is the distance between their centres?
The material of a sphere of radius r is melted and recast into a hollow cylindrical shell of thickness a and outer radius b. What is its length assuming that no material is lost in recasting?
A trader allows a discount of 10% on the marked price of an article and thus gains 17% on the cost price of the article. If the cost price is increased by 10%, then what percentage discount should he allow on the marked price of the article so as to get the same percentage profit as before?
A cube of the maximum possible size is cut from a hemisphere of radius (3√3)/2 cm. One identical cubes is placed next to this cube to form a cuboid. Find the lateral surface area (in cm2) of the cuboid?
7/18 of the balls in a drum were red, 8/15 of the balls in the drum were blue and the rest were yellow. If there were 84 more red balls in that drum than there were yellow balls, what was the total number of balls in the drum?
The ratios of alcohol to water in solutions A and B are 3 ∶ 5 and 9 ∶ 7, respectively. A and B are mixed in the ratio 5 ∶ 8. In 520 ml of the resulting solution, how much water (in ml) should be mixed so as to obtain a solution in which the ratio of alcohol to water is 3 ∶ 4?
The mean of a distribution is 24 and the standard deviation is 6. What is the value of variance coefficient?
A. 50%
B. 25%
C. 100%
D. 75%
Choosing two different numbers from first three natural numbers, the probability of one of the numbers to be maximum of three is
Priyan lent a certain sum of money at a 20% p.a. rate of interest compounded quarterly. If the lender pays three equal quarterly installments of Rs. 1852.2 then find the money lent by Priyan.
|
66 docs|139 tests
|
|
66 docs|139 tests
|