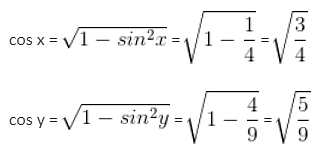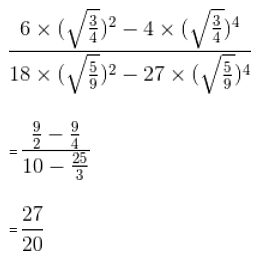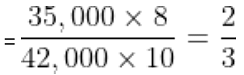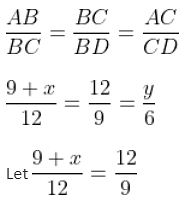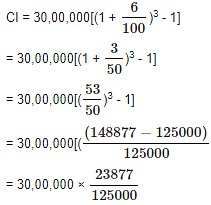SSC CGL (Tier II) Practice Test - 3 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier II Mock Test Series 2024 - SSC CGL (Tier II) Practice Test - 3
If sin x = 1/2 and sin y = 2/3, then what is the value of [(6 cos2 x - 4 cos4 x)/(18 cos2 y - 27 cos4 y)]?
The value of the expression tan 1° tan 2° tan 3° ... tan 89° is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A certain number of men can finish a piece of work in 100 days. If there were 10 men less, it would take 10 days more for the work to be finished. How many men were there?
Reena and Shaloo are partners in a business. Reena invests Rs. 35,000 for 8 months and Shaloo invests Rs. 42,000 for 10 months. Out of a profit of Rs. 31,570, Reena's share will be
The length of a rectangle is 4 cm more than its breadth. If the perimeter of the rectangle is 28 cm, find the length of the rectangle.
A cylindrical tank is filled up to 40% of its capacity. If 160 gallons of water is added to it, then 6/7 of it will be filled. The height of the tank is 4 metres. If the tank is filled with 140 gallons of water, what will be the height of water in the tank?
Directions: Study the information carefully to answer the question that follows.
Number of students that appeared in MBA entrance exam from 2008-2011 = 8,00,000
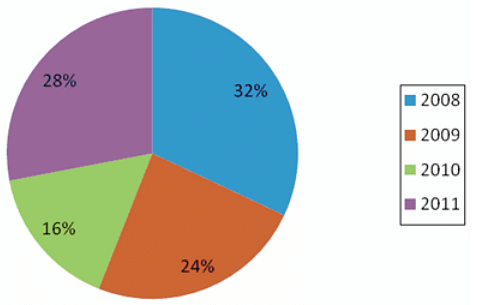
Percentage breakup of number of students that appeared for MBA entrance exam in 2008:
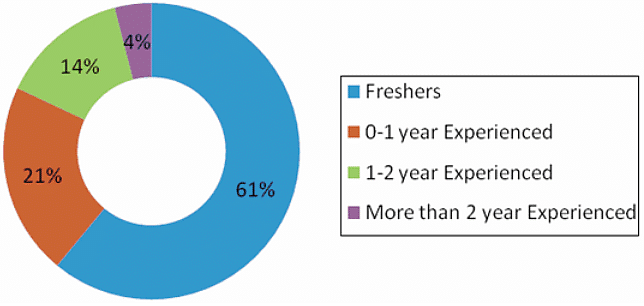
(Note: 0-1 year experienced means the person is having work experience greater than 0 years and up to 1 year.)
Q. If the total students who appeared for MBA entrance exam from 2008-2011 were freshers and 6,15,620 in number, then what percent of them appeared for exam in 2008?
In a club, there are 12 wrestlers. When a wrestler, whose weight is 90 kg, leaves the club, he is replaced by a new wrestler. Then, the average weight of this 12-member club increases by 0.75 kg. What is the weight (in kg) of the new wrestler who joins the club?
Directions: Study the information given below and answer the question that follows.
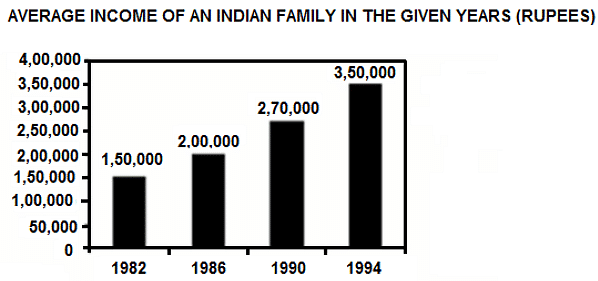

Expenditure is 70%, 75%, 80% and 90% of the income in the years 1982, 1986, 1990 and 1994, respectively.
Q. What is the percentage increase in the income from 1982 to 1990?
A jogger covered a certain distance at some speed. Had he moved 3 km/hr faster, he would have taken 20 minutes less. If he had moved 1 km/hr slower, he would have taken 10 minutes more. What is the distance (in km) that he jogged?
What would be the cost of building a fence around a circular field with area equal to 32378.5 sq. metres, given that the price per metre for building the fence was Rs. 154?
If xyz = 1, yzx = 125, and zyx = 243 (where x, y and z are natural numbers), then what is the value of 9x + 10y - 18z?
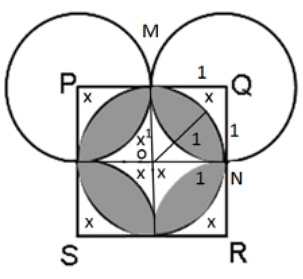
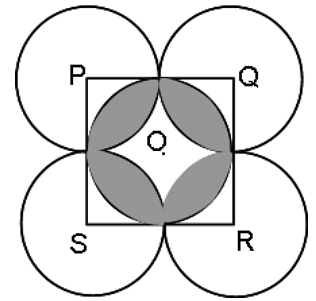
In the given figure, PQRS is a square with side 2 cm. There are 5 equal circles with centres P, Q, R, S and O. Find the area (in sq. cm) of the unshaded part of square PQRS.
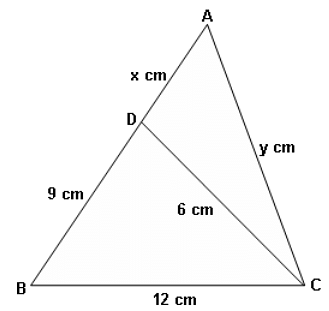
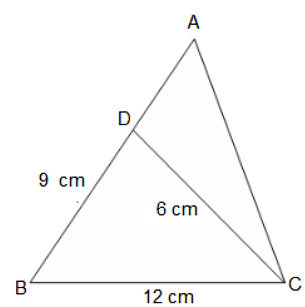
Consider the triangle ABC as shown, where BC = 12 cm, DB = 9 cm, CD = 6 cm and ∠BCD = ∠BAC. What is the ratio of the perimeter of triangle ADC to that of triangle BDC?
A number, when divided by 296, gives 75 as the remainder. If the same number is divided by 37 then the remainder will be
What is the compound interest on RS. 30,00,000 for ![]() years at 12% per annum compounded half - yearly?
years at 12% per annum compounded half - yearly?
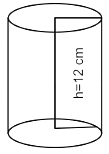
The circumference of the base of a right circular cylinder is 176 cm and its height is 12 cm. Find the total surface area (in cm2) of the cylinder. (Use π = 22/7)
The difference between the compounded interest and the simple interest earned on a certain sum of money in two years at 9% interest per annum is ₹97.2. Find the sum invested.
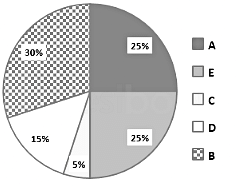
The following pie diagram shows information about tyres manufacturing data from various companies in India during 2017. If the total tyres produced in India during 2017 was 1,80,000 units, how many units of tyres were produced by company ‘D’?
Rakesh secured 92% in a test and Kiran secured 96% in the same test. If the test is conducted out of 375 marks, what is the sum of the marks secured by both Rakesh and Kiran?
The ratio of the length and breadth of the rectangle is 24 : 7. If the diagonal length of the rectangle is 50 cm, then find the area of the rectangle. (in cm2)
Direction: A line graph is given below, study the graph carefully and answer the following questions.
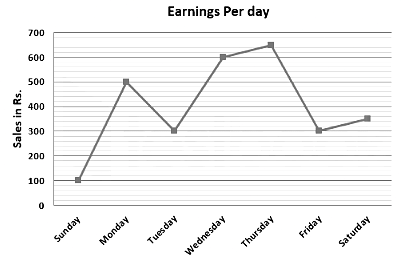
Based on the given graph, the difference in the earnings was the highest between which of the two consecutive days:
The total number of white balls and pink balls is five times the number of blue balls and the total number of pink balls and blue balls are twice the number of white balls. If there are 33 pink balls, then find the total number of balls in the bag.
A batsman scored 84 runs in his 12th innings, thereby improving his average score per innings by 4 runs. What is the average score per innings of the batsman after the 12th innings?
The table shows the production of different types of cars (in thousands).
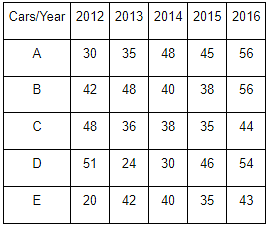
If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector representing the data of production of cars in 2013 will be:
If x (x + y + z) = 30, y (x + y + z) = 64, z (x + y + z) = 50, then find the value of 2(x + y + z), where x, y, z > 0.
A train 225 m long is running at a speed of 145 km/hr. What is the time (in seconds) in which it will pass a man who starts from the engine running at the speed of 17 km/hr in the direction opposite to that of the train?
If (x + 1) ∶ (x + 5) ∶∶ (x + 17) ∶ (x + 53) then what is the mean proportional between (x + 5) and (9x – 1) where x > 0?
The value of 36 ÷ (8 × 3) - [3 ÷ {4 × {3 × 4 ÷ (5 - 9) + 6}}] lies between
How much water should be added to 90 ml of a 38% sugar solution so that it becomes a 17.1% sugar solution?
|
66 docs|139 tests
|
|
66 docs|139 tests
|