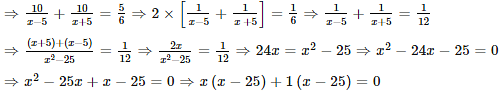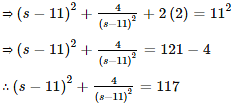SSC CGL (Tier II) Practice Test - 4 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier II Mock Test Series 2024 - SSC CGL (Tier II) Practice Test - 4
The area of an equilateral triangle PQR is 9 times the area of another equilateral triangle XYZ. If perimeter of ΔPQR is 18 cm, what is the length of each side (in cm) of ΔXYZ?
If f(x) = (x - 2)(x2 + Px + 4) and (x - 3) is a factor of f(x), then what is the value of P?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A 64 litre mixture contains water and milk in the ratio 3 : 5. How much water must be added to this mixture to make the ratio 1 : 1?
Directions: Study the given information and answer the following question.
The pie chart given below shows the expenditure on various items and savings of a family during the year 2009.
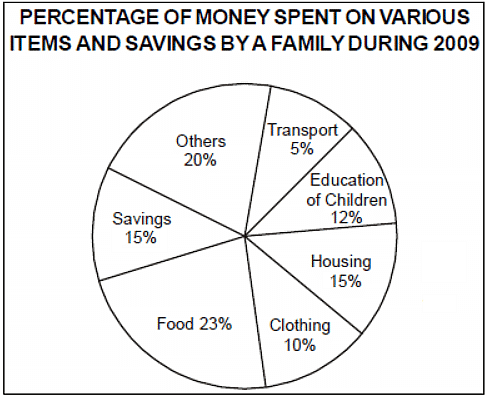
Q. If the total income of the family was Rs. 1,50,000, then the money spent on food was
If 2x = 3y and 2y = 3z, then x : z is equivalent to
PA and PB are two tangents drawn to two circles of radius 3 cm and 5 cm, respectively. PA touches the smaller and larger circles at points X and Y, respectively. PB touches the smaller and large circles at points U and V, respectively. The centres of the smaller and larger circles are O and N, respectively. If ON = 12 cm, then what is the value (in cm) of PY?
Tickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the drawn ticket contains a number, which is a multiple of 3 or 7?
Directions: Study the given information and answer the following question.
The pie chart given below shows the expenditure on various items and savings of a family during the year 2009.

Q. If the total income of the family for the year 2009 was Rs. 1,50,000, then the difference between the expenditures on housing and on transport was
A man can row against the current three-fourth of a kilometre in 15 minutes and returns the same distance in 10 minutes. The ratio of his speed to that of the current is
The ratio between the ages of A and his father is 1 : 7. The difference between their ages is 30 years. What would be the ratio of their ages 10 years later?
A car dealer sold two cars and received $560 for each car. One of these transactions amounted to a 40% profit for the dealer, whereas the other amounted to a 20% loss. What is the dealer's net profit on the two transactions?
Directions: Study the given information and answer the following question.
The pie chart given below shows the expenditure on various items and savings of a family during the year 2009.

Q. The percentage of income which was spent on clothing, education of children and transport together was
A husband and a wife appear in an interview for the same post. The probability of husband's selection is 1/7 and that of wife's selection is 1/5. What is the probability that none of them will be selected?
In a triangle ABC, ∠BAC = 90o and AD is perpendicular to BC. If AD = 6 cm and BD = 4 cm, then the length of BC is
Refer the below data table and answer the following Question.

Q. What was the Revenue of the company if its Expenditure was Rs. 475 crore in the year when its % profit was the least?
In a square, the length of diagonal is 16 cm. The total surface area of a hemisphere is twice the area of square. Find the volume of hemisphere?(in cubic cm) (Use π = 3.14)
If ABC be an equilateral triangle and AD perpendicular to BC Then
AB2 + BC2 + CA2 = ?
Refer the below data table and answer the following Question.

Five points are to be deducted from the student average of marks scored because of poor attendance. What will be the students net average marks scored?
A student appeared for a sectional test containing 10 questions. A reviewer checks the answers and finds that the student answered three questions wrong. What is the probability that the sixth reviewed question is the last wrong question?
Aman goes upstream in a motorboat and returns back to the same point in 50 minutes. If speed of the current is 5 km/hr and total distance travelled by him is 20 km, then what is the speed of the motorboat in still water?
If u : v : w = 1 : 5 : 13, then what will be the value of (3u + 2v + 4w) / (2w - u - 4v)?
The marked price of an article is Rs. 950. A shopkeeper gives a discount of 10% and still makes a profit of 80%. What is the cost price (in Rs.) of the article?
If s2 – 33s + 244 = 0, then, the value of ![]() is__.
is__.
A truck after covering 1 / 6th of the total distance decreases its speed by 2 / 3 of its usual speed and reaches destination 1 hr 40 minutes late. Find the usual time taken (in hours) by the truck to cover the complete distance?
An ore contains 25 % of an alloy that has 90 % iron. Other than this, in the remaining 75% of the ore, there is no iron. How many kilograms of the ore are needed to obtain 60 kg of pure iron?
In a class of 45 students, 40% are girls and the remaining are boys. The average marks of the girls are 64 and that of the boys is 60. What is the average marks of the whole class?
Solutions A and B contain acid and water in the ratio 4 ∶ 3 and 9 ∶ 5, respectively. Four litres of solution A is mixed with 5 litres of solution B. What is the ratio of acid and water in the resulting mixture?
In ΔABC, O is any point inside the triangle. If OA = 12 cm, OC = 15 cm, ∠AOB = ∠BOC = ∠COA and also ∠BAC = 60°. Find OB.
|
66 docs|139 tests
|
|
66 docs|139 tests
|


 = = Rs. 34,500
= = Rs. 34,500
 = 9 : 4
= 9 : 4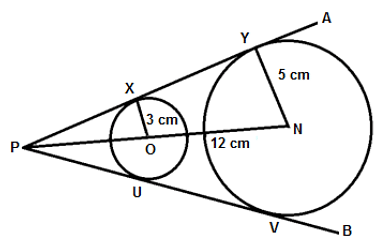



 is equal to
is equal to
 + = $400 + 700 = $1100
+ = $400 + 700 = $1100