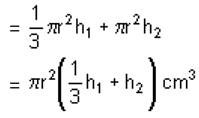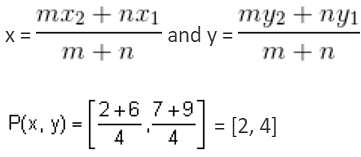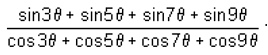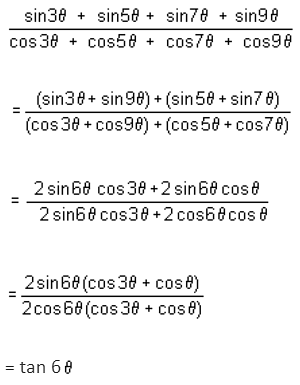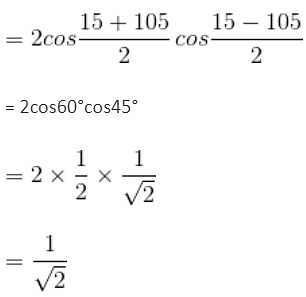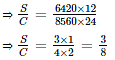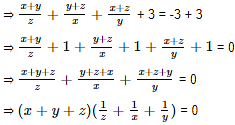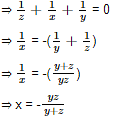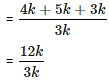SSC CGL (Tier II) Practice Test - 6 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier II Mock Test Series 2024 - SSC CGL (Tier II) Practice Test - 6
What is the sum of all natural numbers between 100 and 400 which are divisible by 13?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a certain test, 4 students each had a score of 80, 10 students each had a score of 70, 4 students each had a score of 75 and 2 students each had a score of 50. What was the average score of 20 students?
If two dice are thrown, what is the probability that the number appeared on second dice is greater than that on the first dice?
If point P(x, y) divides the line segment joining the points (2, 3) and (2, 7) internally in the ratio 1 : 3, then the coordinates of point P are
In how many minimum number of years will a sum of money be more than double at 15% compound interest rate?
x, y and z are positive numbers. If 3x > 9y and 2y > 4z, then which of the following is TRUE?
Directions: Identify the missing number in the given series.
3, 3, 5, ?, 15, 23, 33
What is the value of (x + y) in the given figure, if the perimeter is 34 cm?

Two places A and B are 100 km apart on a highway. One car starts from A and the other from B at the same time. If the cars travel in the same direction at a constant speed, they meet in 5 hours. If the cars travel towards each other, they meet in 1 hour. What is the speed of the car running faster?
Directions: Study the information given below and answer the question that follows.
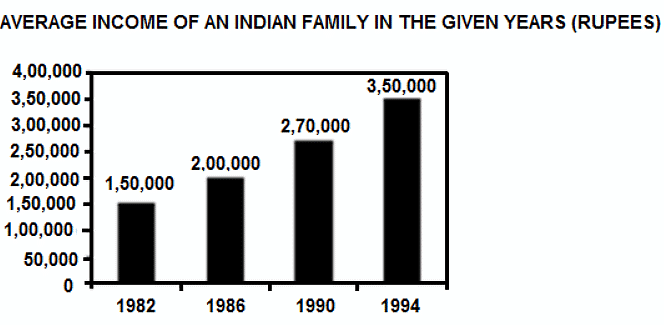

Expenditure is 70%, 75%, 80% and 90% of the income in the years 1982, 1986, 1990 and 1994, respectively.
Q. What was the expenditure on education in the year 1986?
The ratio between the length and breadth of a rectangular field is 5 ∶ 4. If the breadth is 20 metres less than the length, the perimeter of the field is:
5 cot θ + 12 = 0, where π / 2 < θ < π . Find the value of 36 tan θ + 26 sin θ - 39 cos θ
Pipes A and B can fill a tank in 12 hrs and 16 hrs respectively. Whereas pipe C can empty it in 20 hrs. Pipe A and C first opened for 5 hrs and then Pipe A closed and B opened. In how many hours the tank will be filled?
Chand started a business by investing Rs. 8560, after 12 months Sooraj invested Rs. 6420. If the total profit earned by Sooraj and Chand at the end of two years is Rs. 1815, then find the difference in the profit earned by Sooraj and Chand.
If ![]() , where x + y + z ≠ 0, then find the value of x.
, where x + y + z ≠ 0, then find the value of x.
Study the given graph and answer the question that follows.
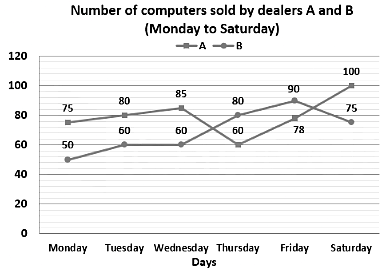
Q. Which of the following statement is correct?
I. The total number of computers sold by dealer A on Monday, Tuesday and Friday is 240.
II. The total number of computers sold by dealer B on Wednesday, Thursday and Saturday is 215.
Which of the following will have the lowest discount percentage?
If x and y are the LCM and HCF of the numbers, 30, 45, 90 and 135 respectively, then what is the value of x - 7y?
Study the following table to answer the questions that are given below.
Expenditures of a company per annum over the given year.

Q. The ratio between the total expenditure on taxes for all the years and the total expenditure on fuel and transport for all years respectively is approximately.
If the number 678967# is exactly divisible by 72, the minimum value of # is:
In ΔPQR, ∠PQR = 90°, PQ = 7 cm, QR = 24 cm. Calculate the radius of the incircle.
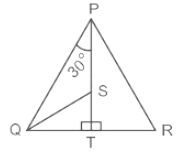
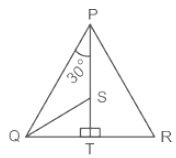
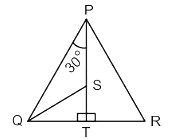
In diagram in ΔPQR, T is a point on the side QR and PT is perpendicular to QR. S is a point on PT in such a way that PS : ST = 3 : 1. If ∠QPT = 30° and tan ∠PRQ = 4 × tan ∠SQT, then find ∠PRQ.
Find the value of 1/(4 - √15) – 1/(√15 - √14) + 1/(√14 - √13) -1/√(13 - √12) + 1/√(12 - √11) – 1/(√11 - √10) + 1/(√10 – 3)
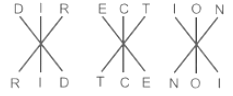
In the following questions, identify the reasoning between the two terms to the left of the mark (∶∶) and select the correct option for each question by applying the same reasoning to both the terms to the right of the mark (∶∶) in each question.
CIGARETTE ∶ GICERAETT ∶∶ DIRECTION ∶ _______
|
66 docs|139 tests
|
|
66 docs|139 tests
|


 (2 × 104 + 22 × 13) = 5681
(2 × 104 + 22 × 13) = 5681