JEE Main 2018 April 8 Shift 1 Paper & Solutions - JEE MCQ
30 Questions MCQ Test - JEE Main 2018 April 8 Shift 1 Paper & Solutions
The density of a material in the shape of a cube is determines by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is :
All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
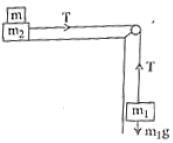
Two masses m1 = 5 kg and m2 = 10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weight m that should be put on top of m2 to stop the motion is :

A particle is moving in a circular path of radius a under the action of an attractive potential 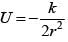 Its total energy is :
Its total energy is :
In a collinear collisio n, a particle with an init ial speed ν0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is:
Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is:
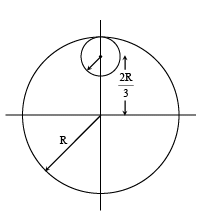
A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then :
A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, (dr/r) is:
Two moles of an ideal monoatomic gas occupies a volume V at 270C. The gas expands adiabatically to a volume 2 V. Calculate (a) the final temperature of the gas and (b) change in its internal energy.
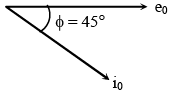
The mass of a hydrogen molecule is 3.32 x 10-27 kg. If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 450 to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly :
A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of 1012/sec. What is the force constant of the bonds connecting one atom with the other ? (Mole wt. of silver = 108 and Avagadro number = 6.02 x 1023 gm mole-1)
A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7 x 103 kg/m3 and its young's modulus is 9.27 x 1010 Pa. What will be the fundamental frequency of the longitudinal vibrations ?
Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge densit ies +σ ,-σ and +σ respectively. The potent ial of shell B is :
A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material constant K = 5/3 is inserted between the plates, the magnitude of the induced charge will be :
In an a.c. circuit, the instantaneous e.m.f. and current are given by:
e = 100 sin 30 t
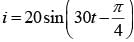 .
.
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively :
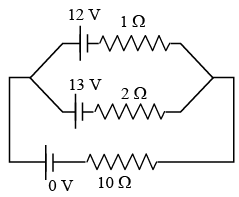
Two batteries with e.m.f. 12 V and 13 V are connected in parallel across a load resistor of 10Ω. The internal resistances of the two batteries are 1Ω and 2Ω respectively. The voltage across the load lies between :
An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii re, rp, rα respectively in a uniform magnetic field B. The relation between re, rp, rα is :
The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2. The ratio B1/B2 is:
For an RLC circuit driven with voltage of amplitude 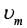 and frequency
and frequency 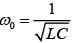 the current exhibits resonance. The quality factor, Q is given by
the current exhibits resonance. The quality factor, Q is given by
An EM wave from air enters a medium. The electric fields are 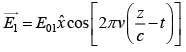 in air and
in air and 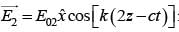 in medium, where the wave number k and frequency
in medium, where the wave number k and frequency 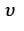 refer to their values in air. The medium is non-magnetic. ∈r1 and ∈r2 refer to relative permitivit ies of air and medium respectively, which of the following options is correct ?
refer to their values in air. The medium is non-magnetic. ∈r1 and ∈r2 refer to relative permitivit ies of air and medium respectively, which of the following options is correct ?
Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be 1/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be 1/8 The angle between polarizer A and C is :
The angular width of the central maximum in a single slit diffraction pattern is 600. The width of the slit is 1μm. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it, Young’s fringes can be observed on a screen placed at a distance of 50 cm from the slits. If the observed fringe width is 1 cm, what is slit separation distance ?
(i.e. distance between the centres of each slit.)
An electron from various excited states of hydrogen atom emit radiation to come to the ground state. Let λn,λg be the de Broglie wavelength of the electron in the nth state and the ground state respectively. Let ∧n be the wavelength of the emitted photon in the transit ion fro m the nth state to the ground state. For large n, (A, B are constants)
If the series limit frequency of the Lyman series is 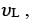 then the series limit frequency of the Pfund series is :
then the series limit frequency of the Pfund series is :
It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is pd; while for its similar collision with carbon nucleus at rest, fractional loss of energy is pc. The values of pd and pc are respectively :
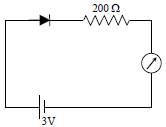
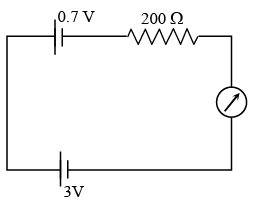
The reading of the ammeter for a silicon diode in the given circuit is :
A telephonic communication service is working at carrier frequency of 10 GHz. Only 10% of it is utilized for transmission. How many telephonic channels can be transmitted simultaneously if each channel requires a bandwidth of 5 kHz ?
In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of 5Ω, a balance is found when the cell is connected across 40 cm of the wire. Find the internal resistance of the cell.
On interchanging the resistances, the balane point of a meter bridge shifts to the left by 10cm. The resistance of their series combinations is 1 kΩ. How much was the resistance on the left slot before interchanging the resistances?




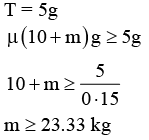

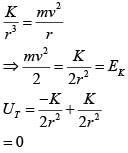
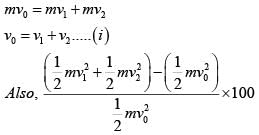
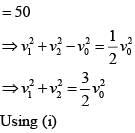
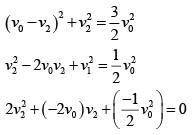
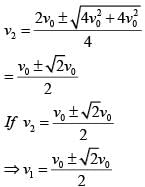
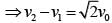
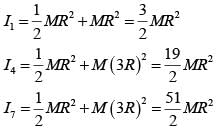
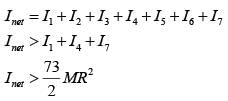
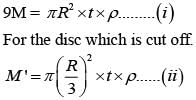
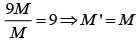
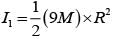
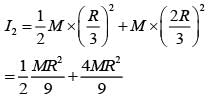
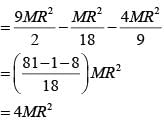
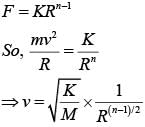
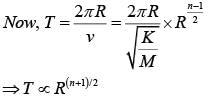
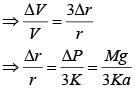
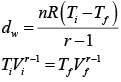

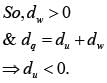
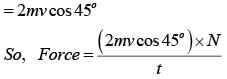
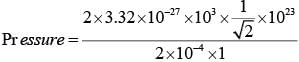
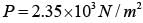
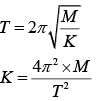
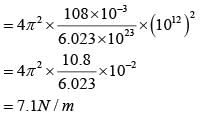
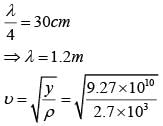
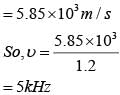
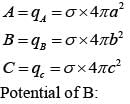
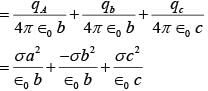
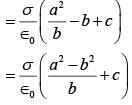
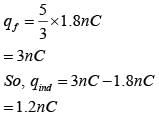
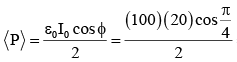
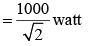
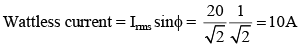
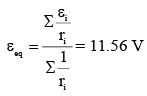
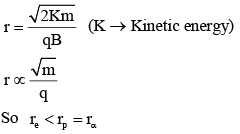
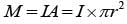 and magnetic field at the centre of circle
and magnetic field at the centre of circle
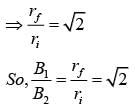
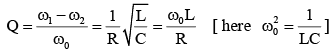
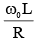 is the only dimensionless quantity, hence must be the quality factor.
is the only dimensionless quantity, hence must be the quality factor.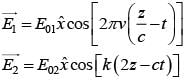
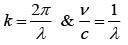
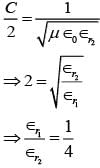
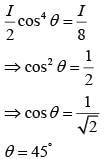
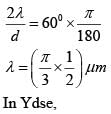
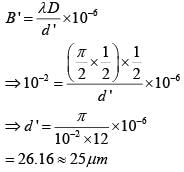
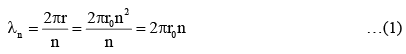
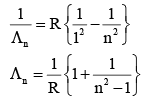
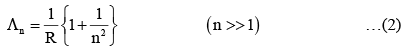
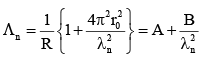




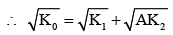 (from conservation of momentum)
(from conservation of momentum)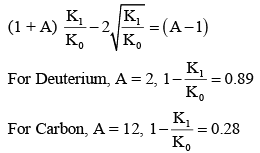
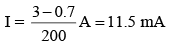
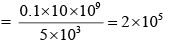
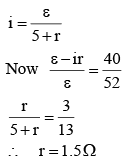
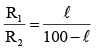 (i)
(i)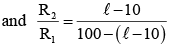 (ii)
(ii)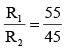 (1)
(1)















