JEE Main Maths Test- 5 - JEE MCQ
25 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Maths Test- 5
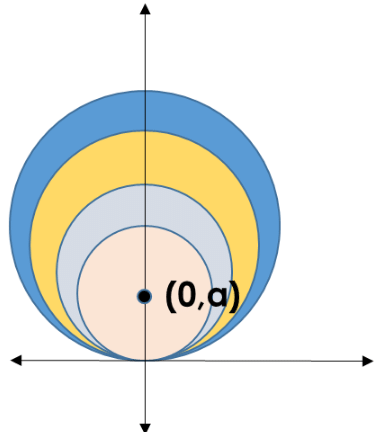
The differential equation of all circles which pass through the origin and whose centres lie on y-axis is
Differential equation for y = A cos αx + B sin αx where A and B are arbitrary constants is
The integrating factor of the different equation dy/dx ( x log x ) + y = 2 log x is given by:
A continuously differentiable function y = f(x) ∈ (0,π ) satisfying y = 1 + y, y (0) = 0 = y(π)is
If 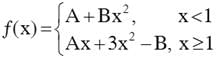 is differentiable at x = 1, then the value of (A + 4B) is
is differentiable at x = 1, then the value of (A + 4B) is
A function y = ƒ(x) satisfies the differential equation 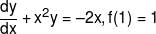 The value of |ƒ"(1)| is
The value of |ƒ"(1)| is
If the foci of the ellipse 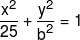 and the hyperbola
and the hyperbola 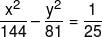 coincide, then the value of b2 is :-
coincide, then the value of b2 is :-
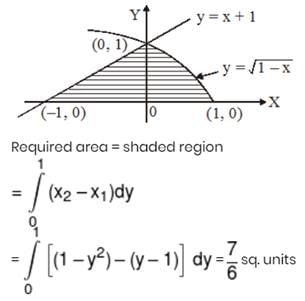
Let f(x) = min.  for all x ≤ 1. Then the area bounded by y = f(x) and the x-axis is :-
for all x ≤ 1. Then the area bounded by y = f(x) and the x-axis is :-
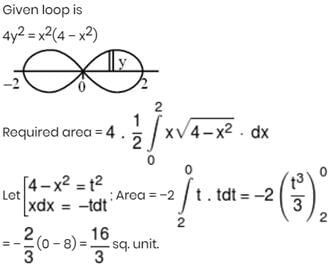
The area bounded by the loop of the curve 4y2 = x2 (4 – x2) is :-
|
356 docs|142 tests
|