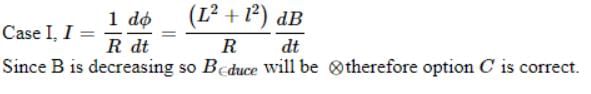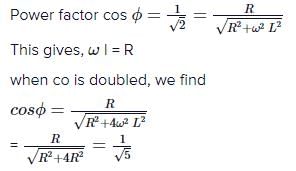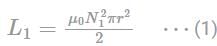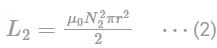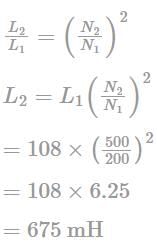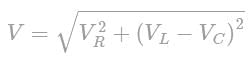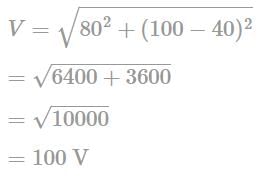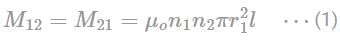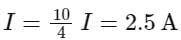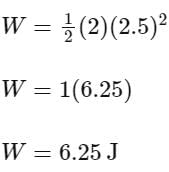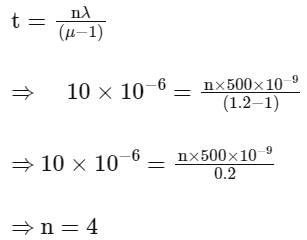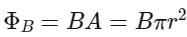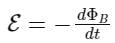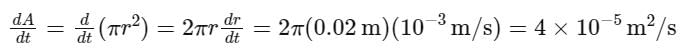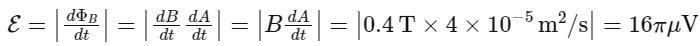JEE Main Part Test - 5 - JEE MCQ
30 Questions MCQ Test - JEE Main Part Test - 5
The magnetic field and number of turns of the coil of an electric generator is doubled then the magnetic flux of the coil will:
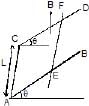
AB and CD are smooth parallel rails, separated by a distance l, and inclined to the horizontal at an angle q. A uniform magnetic field of magnitude B, directed vertically upwards, exists in the region. EF is a conductor of mass m, carrying a current i. For EF to be in equilibrium,
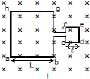
Two different arrangements in which two square wire frames of same resistance are placed in a uniform constantly decreasing magnetic field B.
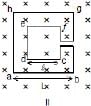
The direction of induced current in the case II is
The power factor of an RL circuit 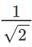 . If the frequency of a.c. is doubled, what will be the power factor?
. If the frequency of a.c. is doubled, what will be the power factor?
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The mirror formula 1/v + 1/u = 1/f is valid for mirrors of small aperture.
Reason (R): Laws of reflection of light is valid for only plane surface and not for large spherical surface.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the objective lens and the eyepiece lens of a microscope are interchanged, it works as a telescope.
Reason (R): Objective lens of telescope require large focal length and eyepiece lens require small focal length.
Which of the following statement is correct regarding AC generators?
In the series LCR circuit, the power dissipation is through:
In the given figure a metallic plate A is allowed to swing like a simple pendulum between the magnetic poles and it comes to rest after time t. If a slot is cut in the plate A and then it is allowed to swing with the same initial velocity as before then the time taken by it to come to rest will be:
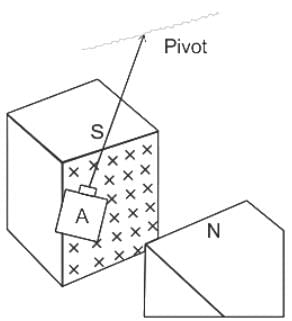
During the magnetic braking of trains if the north and the south poles are replaced with each other, then the velocity of the train will:
A coil of wire of radius R has 200 turns and self – inductance of 108 mH. The self – inductance of a similar coil of 500 turns will be:
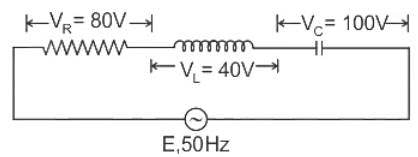
The value of alternating emf E in the given circuit will be:
In the second experiment of Faraday and Henry, the primary coil is connected to the galvanometer and the secondary coil is connected to a battery. If the primary coil is rotated about its axis, then:
When the north pole of a magnet is moved towards a coil that is connected to a circuit, consider the following statement:
a. North pole will be formed on the magnet side of the coil.
b. South pole will be formed on the magnet side of the coil.
c. Direction of Induced current will be clockwise when the coil is seen from the magnet side.
d. Direction of Induced current will be anti-clockwise when the coil is seen from the magnet side.
Two long solenoids S1 and S2 have equal lengths and the solenoid S1 is placed co-axially inside the solenoid S2. If the current in both the solenoids is doubled, then the mutual inductance of both the solenoids will become:
An ideal transformer has 500 and the 1000 turns in the primary and the secondary coil. If the DC voltage of 120 V is applied to the primary coil, then the emf produced at the secondary coil will be:
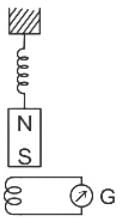
A magnet NS is suspended from a spring and while it oscillates, the magnet moves in and out of the coil. The coil is connected to a galvanometer G. Then, as the magnet oscillates,
Which of the following electromagnetic waves have the longest wavelength?
A coil has an inductance of 2H and resistance of 4Ω. A 10V is applied across the coil. The energy stored in the magnetic field after the current has built up to its equilibrium value will be ___________ × 10−2 J.
A point source of light is placed at the centre of curvature of a hemispherical surface. The source emits a power of 24 W. The radius of curvature of hemisphere is 10 cm and the inner surface is completely reflecting. The force on the hemisphere due to the light falling on it is ____________ × 10−8 N.
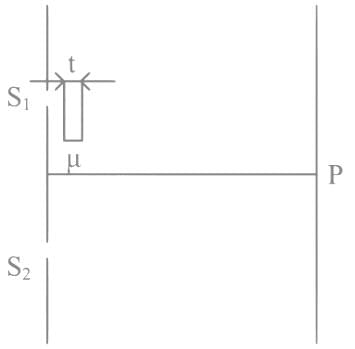
As shown in the figure, in Young's double slit experiment, a thin plate of thickness t = 10μm and refractive index μ = 1.2 is inserted infront of slit S1. The experiment is conducted in air (μ = 1) and uses a monochromatic light of wavelength λ = 500 nm. Due to the insertion of the plate, central maxima is shifted by a distance of x β0. β0 is the fringe-width befor the insertion of the plate. The value of the x is _____________.
A conducting circular loop is placed in a uniform magnetic field of 0.4 T with its plane perpendicular to the field. Somehow, the radius of the loop starts expanding at a constant rate of 1 mm / s . The magnitude of induced emf in the loop at an instant when the radius of the loop is 2 cm will be ___________ μV.
A complex compound in which the oxidation number of a metal is zero is
Trioxalato aluminate (III) and tetrafluorido-borate (III) ions are respectively :
Which of the ligand can show linkage isomerism and acts as flexidentate ligand:
Consider the following statements, "According the Werner's theory. :
(1) Ligands are connected to the metal ions by covalent bonds.
(2) Secondary valencies have directional properties.
(3) Secondary valencies are non-ionisable.
(4) Secondary valencies are satisfied by either neutral or negative legands.
Of these statements.