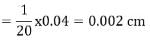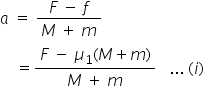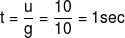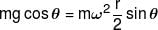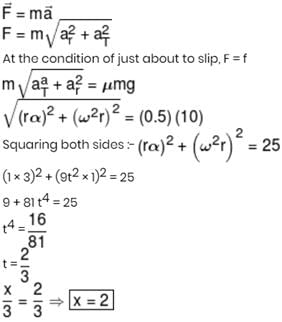Physics Test 1 - Unit And Dimensions, Kinematics, Friction, Laws Of Motion, Work Energy Power
25 Questions MCQ Test JEE Main & Advanced Mock Test Series | Physics Test 1 - Unit And Dimensions, Kinematics, Friction, Laws Of Motion, Work Energy Power
| 1 Crore+ students have signed up on EduRev. Have you? |
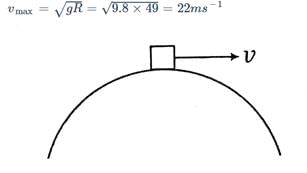
A national roadway bridge over a canal is in the form of an arc of a circle of radius 49 m. What is the maximum speed with which a car can move without leaving the ground at the highest point? (Take g = 9.8 m/second square)
An athlete completes one round of a circular track of radius R in 40 sec. What will be his displacement at the end of 2 min. 20 sec
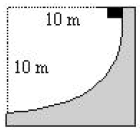
A body slides down a smooth curved track which is the quadrant of a circle having radius 10 m. The speed of the body at the bottom of the track is
A microscope has its main scale with 20 divisions in 1 cm and vernier scale with 25 divisions, the length of which is equal to the length of 24 divisions of main scale. The least count of microscope is:
25* vernier scale reading (vsd) = 24* main scale reading (msd)
1vsd = 0.96 msd
Least count = 1msd - 1vsd=1msd-0.96 msd = 0.04 msd
1 msd = 1/20 cm
So, least count 
A gardener pushes a lawn roller through a distance of 20m. If he applies a force of 20 kg weight in a direction inclined at 60° to the ground, find the work done by him. (g=9.8m/s2)
F = 20kg wt = 20×9.8N
s = 20m
θ = 60°
W = Fscosθ = 20×9.8×20×cos60°
W = 1960J
A particle collides with another particle such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid (m/M= ratio of masses)
Answer :- a,d
Solution :- If nothing is given about the nature of collision, we can not presume it as perfectly elastic. Let e be the coefficient of restitution of collision. For inelastic collision e<1. The collision cannot be perfectly inelastic because the particles do not stick together after collision.
Just after collision
Conservation of linear momentum yields
mv=Mv'
⇒v'/v=m/M
Since e=v'v (numerically)
m/M=e
Since e≤1, m/M≤1
Hence a and d are correct.
One kilometer is equal to how many miles?
If two numerically equal forces P & P acting at a point produce a resultant force of magnitude P itself, then the angle between the two original forces is
The angular velocity (in rad/s) of a body rotating at N r.p.m. is
Angular velocity is defined as the rate of change of angular displacement with respect to time. It is usually expressed by a Greek letter ω (omega).
Mathematically, angular velocity,
ω =dθ/dt
If a body is rotating at the rate of N r.p.m. (revolutions per minute), then its angular velocity,
ω = 2πΝ / 60 rad/s
An object with a mass of 10kg moves at a constant velocity of 10m/s. A constant force then acts for 4 sec on the object and gives it a speed of 2m/sec in opposite direction. The acceleration produced in it is
Change in velocity
-2-10=-12
Time required is 4 seconds
a=Δv/t
=-12/4
=-3 m/s²
Three blocks of masses M1,M2 & M3 are connected by mass-less strings as shown on a friction-less table. They are pulled with a forceT3=40 N. If M1=10kg, M2 = 6kg, M3 = 4kg then TensionT2 will be:
Collision between two carom coins is an example for
The density of material in CGS system of units is 4g/ cm2.In a system of units in which unit of lengths is 10 cm and unit of mass is 100 g, the value of density of material will be
A person is holding a bucket by applying a force of 10N. He moves a horizontal distance of 5m and then climbs up a vertical distance of 10m. Find the total work done by him
F = 10N, s = 5m, θ = 90°
Work done, W1=Fscosθ = 10×5×cos90° = 0
For vertical motion, the angle between force and displacement is 0°.
Here, F = 10N, s = 10m, θ=0°
Work done, W2=10×10×cos0 = 100J
Total work done = W1+W2 = 100J
On the basis of dimensional equation, the maximum number of unknown that can be found, is
Since we define the dimension of the physical quantity into three parameters- mass
Thus we can find maximum of three unknown on the basis of dimensional equation.
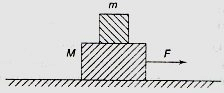
Two blocks of masses M = 5 kg and m = 3 kg are placed on a horizontal surface as shown in this Fig. The coefficient of friction between the blocks is 0.5 and that between the block M and the horizontal surface is 0.7 . What is the maximum horizontal force F that can be applied to block M so that the two blocks move without slipping ?Take g = 10 ms
Let F be the maximum horizontal force that can be applied to block M so that the two blocks move without slipping , i.e. block m doesn't move to backward position.
Lets say, the coefficient of frostion between surface and M is µ1 & that between M and m is µ2
When force F acts on the block combination, friction f acts in the opposite direction as shown in the fig above.
So, the acceleration of the combination
Because of this accelaration, a force F' = ma acts in the opposite direction of accelaration. For this the friction between m and M acts in the same direction of accelaration as shown below.
A particle is projected up a 45° rough incline with a velocity 'v'. The coefficient of friction is 0.5 the speed with which it returns back to the starting point is v1 then v1/v is
A stone is projected upwards from the top of a building with some initial speed and reaches the ground in 5 sec. Now it is allowed to fall with the same initial speed downwards and reaches the ground in 3 sec. If the stone is allowed to fall freely under gravity from the same point, it will reach the ground in
If radian correction is not considered in specific heat measurement. The measured value of specific heat will be
Let the resultant of three forces of magnitude 5N, 12N, & 13N acting on a body be zero. If sin23° = 5/13, then angle between 5N & 13 N force (in degree) will be:
A very large number of balls are thrown vertically upwards in quick succession in such a way that the next ball is thrown when the previous one is at maximum height 5 m. Then number of balls thrown per minute will be :-
For max. height h = 5 m
initial velocity 
So time taken for max-height
So balls are thrown at interval of 1 sec.
So per min. thrown balls are = 60
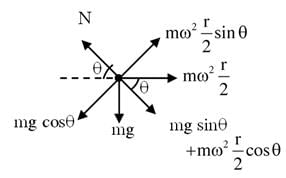
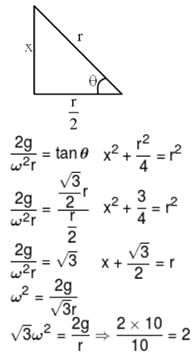
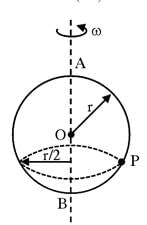
A smooth wire of length 20π m is bent in to a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed ω about the vertical diameter AB, as shown in figure, the bead is at rest with respect to the circular ring at position p as shown. Then the value of √3(ω2) will be:-
When wire is bend to form a circle,
L = 2πr
20π = 2πr
r = 10m.
F.B.D of bead :
As bead is at rest,
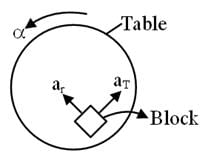
A block of mass m is placed at the distance of 1m from the centre of a round turn table (A table whose surface can rotate about central axis). Table starts from rest and rotates with constant angular acceleration of 3 rad/s2. The coefficient of friction between block and table is µ = 0.5. At time t = x/3 sec from the start of motion the block is just about to slip. Find value of x.
There will be net force due to both the radial and tangential acceleration,
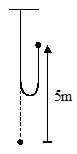
A block of mass 2 kg is suspended from a string, is released from a height of 5m as shown in figure then what will be the impulse when string. Just becomes tight
|
2 videos|324 docs|160 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
2 videos|324 docs|160 tests
|
Download free EduRev App
Related content with Physics Test 1 - Unit And Dimensions, Kinematics, Friction, Laws Of Motion, Work Energy Power
|
|
|
|
Related tests with Physics Test 1 - Unit And Dimensions, Kinematics, Friction, Laws Of Motion, Work Energy Power
|
|
|
|
|
© EduRev
|
Follow Us
|