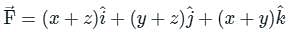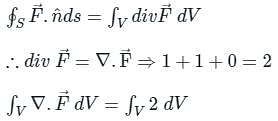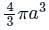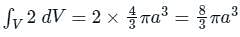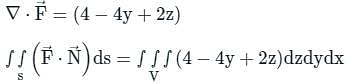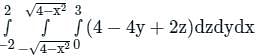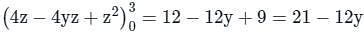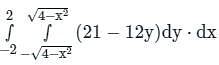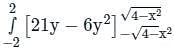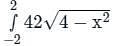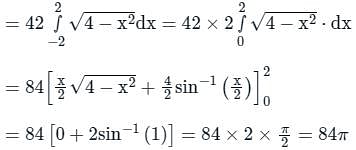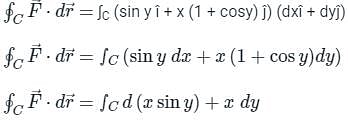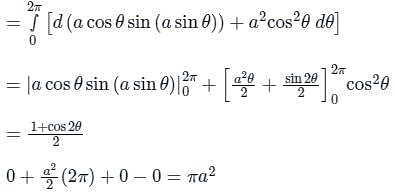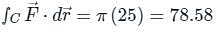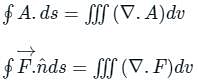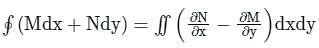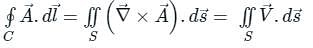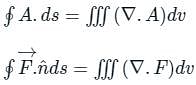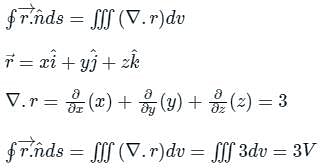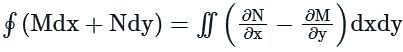Test: Gauss's Theorem - Civil Engineering (CE) MCQ
15 Questions MCQ Test Engineering Mathematics - Test: Gauss's Theorem
Consider a cube of unit edge length and sides parallel to co-ordinate axes, with its centroid at the point (1, 2, 3). The surface integral 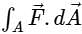 of a vector field
of a vector field 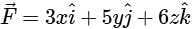 over the entire surface A of the cube is ______.
over the entire surface A of the cube is ______.
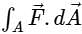 of a vector field
of a vector field 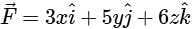 over the entire surface A of the cube is ______.
over the entire surface A of the cube is ______.If C is the plane triangle which is enclosed by the lines x = π/2,y = 2/πx and y = 0, then the value of following integral ∫C[cosxdy + (y − sinx)dx] comes out to be π/a + b/π. Find |ab|
The value of ∫S(x + z)dydz + (y + z)dxdz + (x + y)dxdy, Where ‘S’ is the surface of the sphere x2 + y2 + z2 = 4, is ___
If  and s is the closed surface of x2 + y2 + z2 = a2. Then
and s is the closed surface of x2 + y2 + z2 = a2. Then 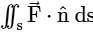 is
is
If S is the surface of the sphere x2 + y2 + z2 = a2, then the value of is
is
By Gauss divergence theorem the value of 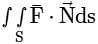 where
where  and S is x2 + y2 = 4, z = 0, z = 3 is
and S is x2 + y2 = 4, z = 0, z = 3 is
Evaluate the line integral of vector field F = sin y î + x (1 + cos y) ĵ along the circular path given by x2 + y2 = a2, z = 0 (Use a = 5 and round-off to two decimals)
Evaluate the surface integral ∫∫ (3x i + 2y j). dS, where S is the sphere given by x2 + y2 + z2 = 9.
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure . All the three charges are positive. The force on the central charge due to the shell is
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
The value of the integral 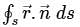 over the closed surface S bounding a volume V, where
over the closed surface S bounding a volume V, where 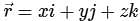 is the position vector and n̂ is normal to the surface S, is
is the position vector and n̂ is normal to the surface S, is
|
65 videos|122 docs|94 tests
|


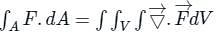
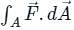 is called surface integral
is called surface integral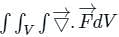 is called volume integral
is called volume integral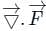 is called divergence of F
is called divergence of F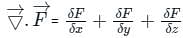

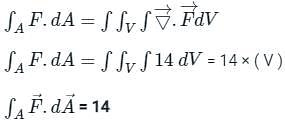

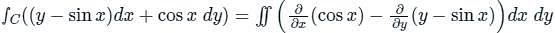


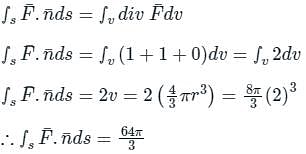

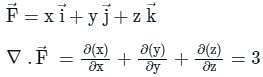
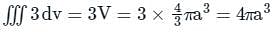
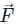 taken around a closed surface S is equal to the integral of the divergence of
taken around a closed surface S is equal to the integral of the divergence of 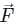 taken over the volume V enclosed by the surface S. Mathematically;
taken over the volume V enclosed by the surface S. Mathematically;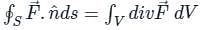
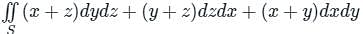 and x2 + y2 + z2 = a2
and x2 + y2 + z2 = a2