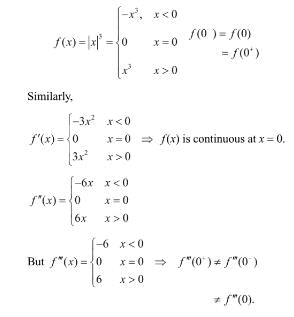Engineering Mathematics Exam > Engineering Mathematics Tests > Engineering Mathematics > Test: Theorems of Integral Calculus- 1 - Engineering Mathematics MCQ
Test: Theorems of Integral Calculus- 1 - Engineering Mathematics MCQ
Test Description
20 Questions MCQ Test Engineering Mathematics - Test: Theorems of Integral Calculus- 1
Test: Theorems of Integral Calculus- 1 for Engineering Mathematics 2025 is part of Engineering Mathematics preparation. The Test: Theorems of Integral Calculus- 1 questions and answers have been
prepared according to the Engineering Mathematics exam syllabus.The Test: Theorems of Integral Calculus- 1 MCQs are made for Engineering Mathematics 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Theorems of Integral Calculus- 1 below.
Solutions of Test: Theorems of Integral Calculus- 1 questions in English are available as part of our Engineering Mathematics for Engineering Mathematics & Test: Theorems of Integral Calculus- 1 solutions in
Hindi for Engineering Mathematics course. Download more important topics, notes, lectures and mock
test series for Engineering Mathematics Exam by signing up for free. Attempt Test: Theorems of Integral Calculus- 1 | 20 questions in 60 minutes | Mock test for Engineering Mathematics preparation | Free important questions MCQ to study Engineering Mathematics for Engineering Mathematics Exam | Download free PDF with solutions
Test: Theorems of Integral Calculus- 1 - Question 1
As x is increased from – ∞ to ∞ , the function
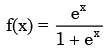
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 1
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 2
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 3
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 4
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 5
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 6
Test: Theorems of Integral Calculus- 1 - Question 7
Which of the following functions is not differentiable in the domain [-1,1]?
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 7
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 8
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 9
Test: Theorems of Integral Calculus- 1 - Question 10
What should be the value of λ such that the function defined below is continuous at x = π/2?
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 10
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 11
Test: Theorems of Integral Calculus- 1 - Question 12
Consider the function f(x) = |x|3, where x is real. Then the function f(x) at x = 0 is
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 12
Test: Theorems of Integral Calculus- 1 - Question 13
The expression e–ln x for x > 0 is equal to
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 13
Test: Theorems of Integral Calculus- 1 - Question 14
Consider the following two statements about the function f(x) = |x|
P: f(x) is continuous for all real values of x
Q: f(x) is differentiable for all real values of x
Which of the f oll owi ng is TRU E?
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 14
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 15
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 16
Test: Theorems of Integral Calculus- 1 - Question 17
Which one of the following function is strictly bounded?
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 17
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 18
Test: Theorems of Integral Calculus- 1 - Question 19
Which of the following integrals is unbounded?
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 19
Test: Theorems of Integral Calculus- 1 - Question 20
What is the value of the definite integral,
Detailed Solution for Test: Theorems of Integral Calculus- 1 - Question 20
|
65 videos|133 docs|94 tests
|
Information about Test: Theorems of Integral Calculus- 1 Page
In this test you can find the Exam questions for Test: Theorems of Integral Calculus- 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Theorems of Integral Calculus- 1, EduRev gives you an ample number of Online tests for practice