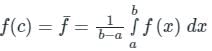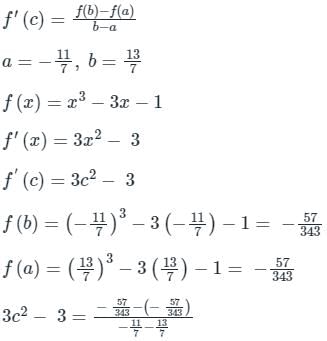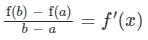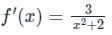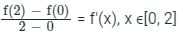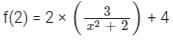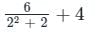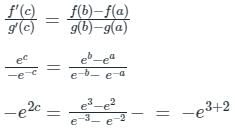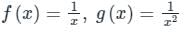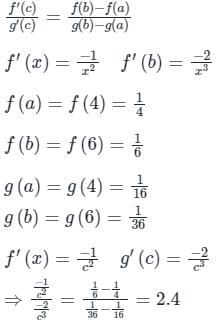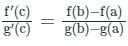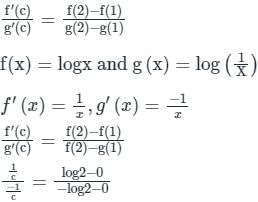Test: Mean Value Theorem - Engineering Mathematics MCQ
10 Questions MCQ Test Engineering Mathematics - Test: Mean Value Theorem
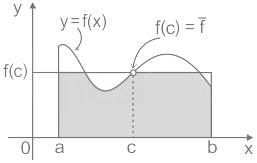
The mean value of a function f(x) from point ‘a’ to point ‘b’ is given by
If f(x) = x3 − 3x − 1 is continuous in the closed interval 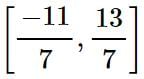 and f’(x) exists in the open interval
and f’(x) exists in the open interval 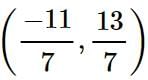 then find the value of 'c' such that it lies in
then find the value of 'c' such that it lies in 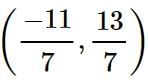 ?
?
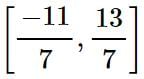 and f’(x) exists in the open interval
and f’(x) exists in the open interval 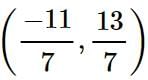 then find the value of 'c' such that it lies in
then find the value of 'c' such that it lies in 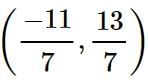 ?
?If f(0) = 4 and f'(x) = 3 / x2 + 2, the lower bound of f(2) estimated by mean value theorem is
The value of ‘c’ of the Cauchy’s mean value theorem for f(x) = ex and g(x) = e-x in [2, 3] is _____.
Find C of Cauchy’s mean value theorem for the function 1/x and 1/x2 in [4, 6]
The mean value c for the function f(x) = logx and g(x) = log(1/X) in [1, 2] is
If f and g are differentiable functions in (0, 1) satisfying f(0) = 2 = g(1), g(0) = 0 and f(1) = 6, then for some c ϵ (0, 1)
If a continuous function f(x) does not have a root in the interval [a, b], then which one of the following statements is TRUE?
If f(x) is a linear function in the interval [−3, 3] then the value of c for c∈(−3, 3) such that 6f′(c) + f(−3) = f(3).
|
65 videos|133 docs|94 tests
|


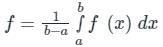
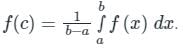
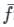 :
: