Test: Force & Newton's Laws of Motion - 1 - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: Force & Newton's Laws of Motion - 1
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. If a force of 2.8 N is applied on the block parallel to floor, the force of friction between the block and floor is (Take g = 10 m/s2)
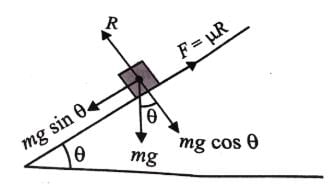
A block has been placed on an inclined plane. The slope angle θ of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is equal to
A body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficients of static and kinetic frictions 0.5 and 0.4 respectively. On applying the same force, what is the acceleration?
`A 40 kg slab rests on a frictionless floor. A 10 kg block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient is 0.40. The 10 kg block is acted upon by a horizontal force of 100 N. If g = 9.8 m/s2 the resulting acceleration of the slab will be
If the coefficient of friction of a surface is μ = √3, then the angle of inclination of a plane to make a block on it to just start sliding is
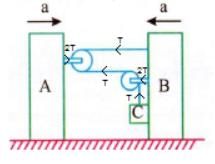
If A and B moves with acceleration ‘a’ as shown in diagram, calculate acceleration of C with respect to B
A block takes twice as much time to slide down a 45o rough inclined plane as it takes to slide down a similar smooth plane. The coefficient of friction is
The acceleration that is produced by a 15N force in a mass of 8 kg will be equal to
A block of mass 6 kg is being pulled by force 24 N as shown. If coefficient of friction between block and the surface is 0.6, frictional force acting on the block is
In figure, coefficient of friction between m1 and m2 is m and that between m1 and the wall is zero. A force F is pressing the system against the wall. Minimum value of force required to hold the system in equilibrium is
A body moves along a circular path of radius 5 m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g = 10 m/s2)
In figure, coefficient of friction between m2 and the horizontal surface is μ, minimum value of m so that the system has zero acceleration, is
A uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is
A man of mass m stands on a platform of equal mass m and pulls himself by two ropes passing over pulleys as shown in figure. If he pulls each rope with a force equal to half his weight, his upward acceleration would be
The car A is used to pull a load B with the pulley arrangement shown. If A has a forward velocity v determine an expression for the upward velocity vB of the load in terms of vA and θ.θ is angle between string and horizontal
A man slides down on a telegraphic pole with an acceleration equal to one-fourth of acceleration due to gravity. The frictional force between man and poles is equal to (in terms of man’s weight w)
A cart of mass M has a block of mass m attached to its as shown in the figure. The coefficient of friction between the block and cart is μ. The minimum acceleration of the cart so that the block m does not fall is
A block is placed on a rough surface and an external horizontal force F is applied on it. The force of friction ‘f’ exerted by the floor on the block is measured for different values of F. The graph between F and f is
If the coefficient of friction between an insect and bowl surface is μ and the radius of the bowl is r, the maximum height to which the insect can crawl in the bowl is
A block rests on a rough inclined plane making an angle of 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (Take g = 10 m/s2)
Pulleys and strings are massless. The horizontal surface is smooth. What is the acceleration of the block
A ball of mass 0.5 kg is attached to the end of a string having length 0.5 m. The hall is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball in (rad/s)
In the pulley-block arrangement shown in figure, find the relation between acceleration of block A and B
The limiting friction between two surface does not depend
A body is sliding down a rough inclined plane of inclination 60o. If the angle of repose is 30o, the acceleration of the body (g = 10 m/s2) in m/s2 is
A cyclist of mass 30 kg exerts a force of 250 N to move his cycle. acceleration is 4 ms−2. force of friction between road and tyres will be
A conveyor belt is moving at a constant speed of 2 m/s. A box is gently dropped on it. The coefficient of friction between them is m = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g = 10 m/s2, is
A block of weight 100 N is pushed by a force F on a horizontal rough plane moves with an acceleration 1 m/s2, when force is doubled its acceleration becomes 10 m/s2. The coefficient of friction is (g = 10 m/s2)
What is the smallest radius of a circle at which a bicyclist can travel if his speed is 7 m/s and the coefficient of static friction between tyres and road is 0.25
|
481 docs|964 tests
|