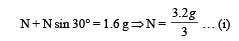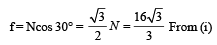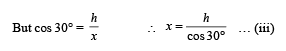JEE Advanced (Single Correct MCQs): Rotational Motion - JEE MCQ
26 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Rotational Motion
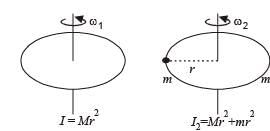
A thin circular ring of mass ‘M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m,, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity
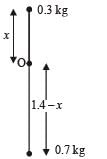
Two point masses of 0.3 kg and 0.7 kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and centre of mass velocity ν. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB, respectively. Then
A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin O is
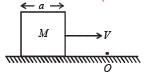
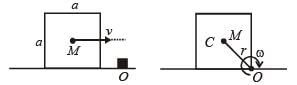
A cubical block of side a is moving with velocity V on a horizontal smooth plane as shown in Figure. It hits a ridge at point O. The angular speed of the block after it hits O is
A long horizontal rod has a bead which can slide along its length and initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration a . If the coefficient of friction between the rod and the bead is m , and gravity is neglected, then the time after which the bead starts slipping is
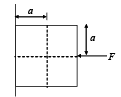
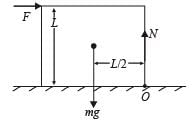
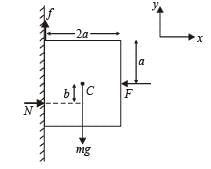
A cubical block of side L rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
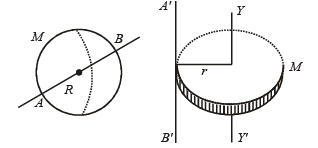
A thin wire of length L and uniform linear mass density r is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
An equilateral triangle ABC formed from a uniform wire has two small identical beads initially located at A. The triangle is set rotating about the vertical axis AO. Then the beads are released from rest simultaneously and allowed to slide down, one along AB and the other along AC as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are
One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the center of the original disc. Its moment of inertia about the axis of rotation is
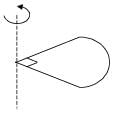
A cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platformω(t) will vary with time t as
Consider a body, shown in figure, consisting of two identical balls, each of mass M connected by a light rigid rod. If an impulse J=MV is imparted to the body at one of its ends, what would be its angular velocity?
A particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
A horizontal circular plate is rotating about a vertical axis passing through its centre with an angular velocity ωo. A man sitting at the centre having two blocks in his hands stretches out his hands so that the moment of inertia of the system doubles. If the kinetic energy of the system is K initially, its final kinetic energy will be
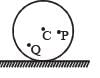
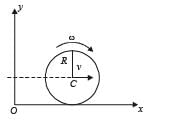
A disc is rolling without slipping with angular velocity w. P and Q are two points equidistant from the centre C. The order of magnitude of velocity is
A block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
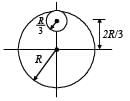
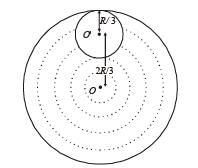
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The m oment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
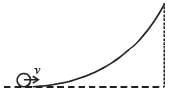
A particle is confined to rotate in a circular path decreasing linear speed, then which of the following is correct?
A solid sphere of mass M and radius R having moment of inertia I about its diameter is recast into a solid disc of radius r and thickness t. The moment of inertia of the disc about an axis passing the edge and perpendicular to the plane remains I. Then R and r are related as
A small object of uniform density rolls up a curved surface with an initial velocity v. It reaches up to a maximum height of 3v2/4g with respect to the initial position. The object is
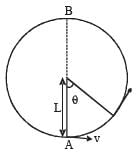
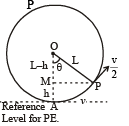
A bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies –
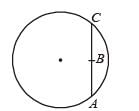
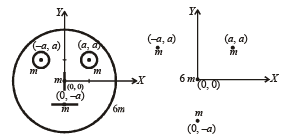
Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6 m.The coordinates of the centres of the different parts are: outer circle (0, 0), left inner circle (– a, a), right inner circle (a, a), vertical line (0, 0) and horizontal line (0, – a). The y-coordinate of the centre of mass of the ink in this drawing is
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed w. If the angular momentum of the system, calculated about O and P are denoted by 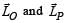 respectively, then
respectively, then
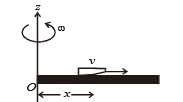
A thin uniform rod, pivoted at O, is rotating in the horizontal plane with constant angular speed ω, as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v, with respect to the rod towards the other end. It reaches the end of the rod at t = T and stops. The angular speed of the system remains w throughout. The magnitude of the torque about O, as a function of time is best represented by which plot?
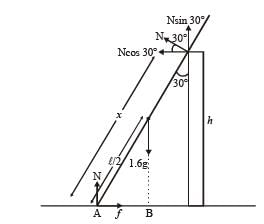
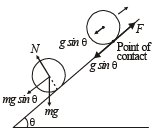
A uniform wooden stick of mass 1.6 kg and length l rests in an inclined manner on a smooth, vertical wall of height h(< l) such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of 30° with the wall and the bottom of the stick is on a rough floor.
The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/l and the frictional force f at the bottom of the stick are (g = 10 m s–2)



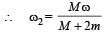
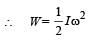
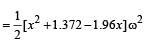
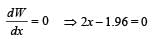
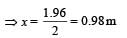

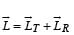
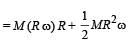
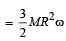
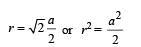
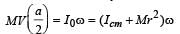
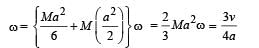
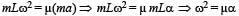
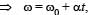
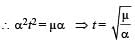
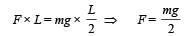
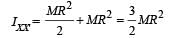
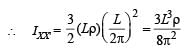
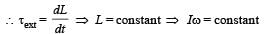

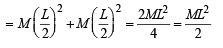
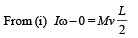
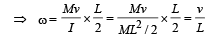
 The total mass of the disc
The total mass of the disc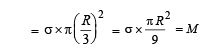
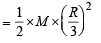
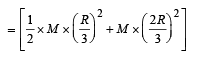
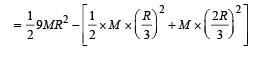
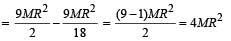
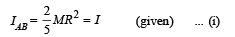
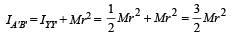
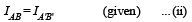 .
.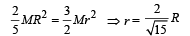
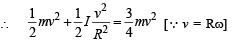
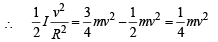
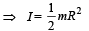
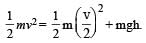
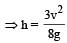
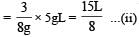
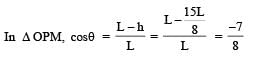
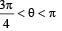
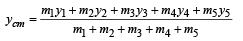
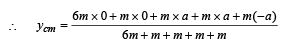
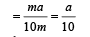
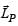 remains changing for different locations of m.
remains changing for different locations of m.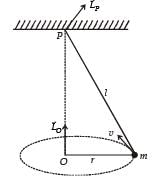
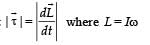


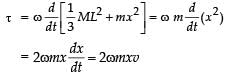


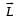 does not change and therefore τ becomes constant.
does not change and therefore τ becomes constant.