Test: Congruence Criteria- SAS And ASA - Grade 9 MCQ
15 Questions MCQ Test - Test: Congruence Criteria- SAS And ASA
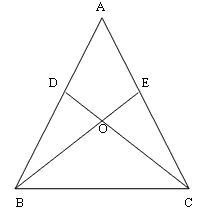
In the given figure, AB = AC, AD = AE = 5 cm and DC = 8 cm. Length of EB is______.
Triangle ABC is congruent to triangle DEF. Which side is congruent to side BC?
Which of the following statements is incorrect ?
In the following figure, PQ = PR and SQ = SR, then
If two triangles ABC and PQR are congruent under the correspondence A ↔ P, B ↔ Q and C ↔ R, then symbolically, it is expressed as
If ΔABC ≌ ΔPQR then, which of the following is true?
If two sides of a triangle are equal, the angles opposite to these sides are______.
In case of two equilateral triangles, PQR and STU which of the following correspondence is not correct?
In quadrilateral ADBC, AB bisects ∠A. Which of the following criterion will prove ΔABC ≅ ΔABD?
In an isosceles triangle ABC with AB = AC, if BD and CE are the altitudes, then BD and CE are______.
In fig., if AB = AC and PB = QC, then by which congruence criterion PBC ≅ QCB
The diagonal PR of a quadrilateral PQRS bisects the angles P and R, then
In the given figure, AB = EF, BC = DE, AB ⊥ BD and EF ⊥ CE. Which of the following criterion is true for ΔABD ≅ ΔEFC?
Two figures are congruent if they have______.














