Test: Types And Angle Sum Property - Class 9 MCQ
10 Questions MCQ Test - Test: Types And Angle Sum Property
The opposite angles of a parallelogram are (3x – 2)° and (50 – x)° the measure of these angles is
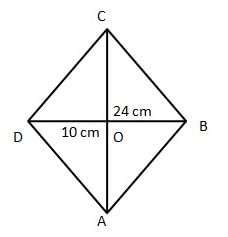
The diagonals of a rhombus are 10 cm and 24 cm. find the length of a side of the rhombus.
In quadrilateral PQRS, if ∠P = 60° and ∠Q : ∠R : ∠S = 2 : 3 : 7, then ∠S =
The angles of a quadrilateral are (5x)°, (3x + 10)°, (6x – 20)° and (x + 25)°. Now, the measure of each angle of the quadrilateral will be
The angles of a quadrilateral are in the ratio 3:5:9:13. The measure of angles of quadrilateral are:
Two angles of a quadrilateral are 50° and 80° and other two angles are in the ratio 8 : 15. Find the measure of the remaining two angles.
All the angles of a convex quadrilateral are congruent. However, not all its sides are congruent. What type of quadrilateral is it?
The type of polygon in which its all angles and sides are equal is classified as