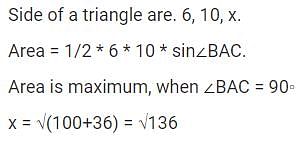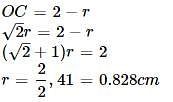Test: Geometry- 2 - UPSC MCQ
15 Questions MCQ Test CSAT Preparation - Test: Geometry- 2
A cyclic quadrilateral is such that two of its adjacent angles are divisible by 6 and 10 respectively. One of the remaining angles will necessarily be divisible by:
The volume of two spheres are in the ratio 27 : 125. The ratio of their surface area is?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Sides of a triangle are 6, 10 and x for what value of x is the area of the △ the maximum?
A square is inscribed in a semi circle of radius 10 cm. What is the area of the inscribed square? (Given that the side of the square is along the diameter of the semicircle.)
Two circles of an equal radii are drawn, without any overlap, in a semicircle of radius 2 cm. If these are the largest possible circles that the semicircle can accommodate, what is the radius (in cm) of each of the circles?
PQRS is a Trapezzium, in which PQ is Parralel to RS, and PQ = 3 (RS) . The diagnol of the Trapezzium intersect each other at X, then the ratio of, ar ( ∆ PXQ) : ar ( ∆ RXS) is?
Let ABCDEF be a regular hexagon. What is the ratio of the area of the triangle ACE to that of the hexagon ABCDEF?
A pond 100 m in diameter is surrounded by a circular grass walk-way 2 m wide. How many square metres of grass is the on the walk-way?
The dimensions of a rectangular box are in the ratio of 1:2:4 and the difference between the costs of covering it with the cloth and a sheet at the rate of Rs 20 and Rs 20.5 per sq m respectively is Rs 126. Find the dimensions of the box.
The ratio of the area of a square inscribed in a semicircle to that of the area of a square inscribed in the circle of the same radius is
The ratio of the area of a square to that of the square drawn on the its the diagonal is
What is the area of the triangle in which two of its medians 9 cm and 12 cm long intersect at the right angles?
Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.
Two sides of a triangle are 4 and 5. Then, for the area of the triangle, which one of the following bounds is the sharpest?
|
218 videos|139 docs|151 tests
|