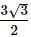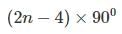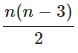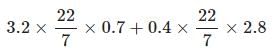Test: Polygons - UPSC MCQ
15 Questions MCQ Test UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making - Test: Polygons
Find the number of sides of a polygon if the sum of its interior angles is equal to 18000?
What is the measure of each interior angle of a regular hexagon (in degrees)?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
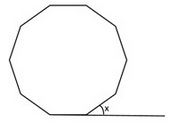
The figure below is a regular polygon. Find the measure of angle x (in degrees)?
If ABCDEF is a regular hexagon and AB = 1cm, then what is the area of this regular hexagon ABCDEF?
The area of polygon ABCD is equal to 8√3 cm2. If triangle ABD and BCD are equilateral triangles, then find the perimeter of the polygon ABCD?
ABCDE is a regular pentagon. Sides AE and ED of the pentagon are extended as shown to form triangle EFG, which is right-angled at F. Vertices A and C are joined to form the triangle ABC. What is the value of sum (x° + y°)?
The above shape is made of eight identical equilateral triangles, each having a perimeter of 3. What is the straight-line distance between points P and Q?
Corners of an equilateral triangle were cut off such that a regular hexagon is formed. If each side of the original triangle measures 9 cm, find the area of the hexagon in square cm.
Dodger’s stadium, which is rectangular in shape, currently has one parking lot that has a maximum capacity of 2000 cars. In order to accommodate the increased demand due to District Level games, the management plans to increase the capacity of the parking lot by adding one more parking lot – parking lot 2. Assuming the shape of the structure as shown in the figure, what is the ratio of the width of parking lot 2 (w2) to the width of parking lot 1(w1). Also assume that the height of both the triangular parking lots is same as the width of the rectangle and that the allowed spacing between the cars is same in both parking lots.
(1) After the addition of parking lot 2, the total parking capacity of the stadium is 6000 cars.
(2) The area of parking lot 1 is 10000 m2
Two identical regular hexagons are inscribed in a rectangle whose area is 256√3 square inches. What is the perimeter of each hexagon in inches?
A regular polygon is partially obscured by a box. What is the sum of the angles of the polygon?
(1) x°= y°
(2) x°+ y°= 72°
If the sum of interior angles of a polygon is 900 degrees, what is the number of diagonals it has?
In a regular pentagon PQRST, what is the ratio of the area of triangle PRS to the area of the pentagon PQRST?
A regular polygon P has 135 diagonals. Find the exterior angle of the polygon P.
A cylindrical pencil consists of a layer of wood surrounding a solid cylinder of graphite. The radius of the pencil is 6 mm, the radius of the graphite cylinder is 2 mm and the length of the pencil is 10 cm. Find the cost of the material used in a pencil, if the cost of wood is Rs. 0.70/cm3 and that of graphite is Rs. 2.80/cm3.
|
67 videos|50 docs|151 tests
|
|
67 videos|50 docs|151 tests
|