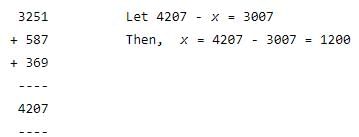Test: Unit Digits- 3 - UPSC MCQ
10 Questions MCQ Test UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making - Test: Unit Digits- 3
Given that a, b, c, and d are different nonzero digits and that 10d + 11c < 100 – a, which of the
following could not be a solution to the addition problem below?
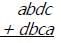
following could not be a solution to the addition problem below?
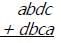

If k and p represent non-zero digits within the integers above, what is p?

If k and p represent non-zero digits within the integers above, what is p?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x represents the sum of all the positive three-digit numbers that can be constructed using each of the
distinct nonzero digits a, b, and c exactly once, what is the largest integer by which x must be divisible?
distinct nonzero digits a, b, and c exactly once, what is the largest integer by which x must be divisible?
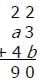
If a and b represent positive single digits in the correctly worked computation above, what is the value of the two digit integer ba?
For any four digit number, abcd, *abcd*= (3a)(5b)(7c)(11d). What is the value of (n – m) if m and n are fourdigit numbers for which *m* = (3r)(5s)(7t)(11u) and *n* = (25)(*m*)?
|
67 videos|50 docs|151 tests
|
|
67 videos|50 docs|151 tests
|


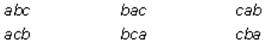
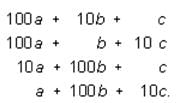
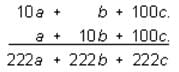
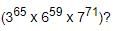
 Unit digit in (34)16 = 1
Unit digit in (34)16 = 1 Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3
Unit digit in 365 = Unit digit in [ (34)16 x 3 ] = (1 x 3) = 3 Unit digit in (74)17 is 1.
Unit digit in (74)17 is 1. Required digit = Unit digit in (3 x 6 x 3) = 4.
Required digit = Unit digit in (3 x 6 x 3) = 4.