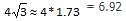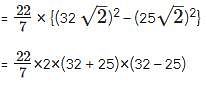Test: Mensuration, Solid Geometry Questions - CLAT MCQ
20 Questions MCQ Test Quantitative Techniques for CLAT - Test: Mensuration, Solid Geometry Questions
A 5 cubic centimeter cube is painted on all its side. If it is sliced into 1 cubic centimer cubes, how many 1 cubic centimeter cubes will have exactly one of their sides painted?
The area of a square field is 24200 sq m. How long will a lady take to cross the field diagonally at the rate of 6.6 km/hr?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The circumference of the front wheel of a cart is 30 ft long and that of the back wheel is 36 ft long. What is the distance travelled by the cart, when the front wheel has done five more revolutions than the rear wheel?
If the sides of a triangle measure 72, 75 and 21, what is the measure of its in radius?
A 5 cm cube is cut into as many 1 cm cubes as possible. What is the ratio of the surface area of the larger cube to that of the sum of the surface areas of the smaller cubes?
If each interior angle of a regular polygon is 150 degrees, then it is a/an ______________
Four horses are tethered at 4 corners of a square field of side 70 metres so that they can just about reach one another. The area left ungrazed by the horses is:
A square sheet of paper is converted into a cylinder by rolling it along its length. What is the ratio of the base radius to the side of the square?
The surface area of the three coterminous faces of a cuboid are 6, 15, 10 sq.cm respectively. Find the volume of the cuboid.
If the diagonal and the area of a rectangle are 25 m and 168 m2, what is the length of the rectangle?
A 4 cm cube is cut into 1 cm cubes. What is the percentage increase in the surface area after cutting?
A regular hexagon is inscribed in a circle of radius r cm. What is the perimeter of the regular hexagon?
If x units are added to the length of the radius of a circle, what is the number of units by which the circumference of the circle is increased?
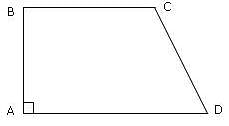
ABCD has area equal to 28. BC is parallel to AD. BA is perpendicular to AD. If BC is 6 and AD is 8, then what is CD?
Which of the following figures has the largest area?
A circle of radius √2
An equilateral triangle whose sides each have length 4
A triangle whose sides have lengths 3, 4 and 5
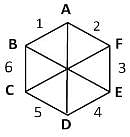
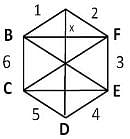
The hexagon ABCDEF is regular. That means all its sides are of the same length and all its interior angles are of the same size. Each side of the hexagon is 2 m. What is the area of the rectangle BCEF?

Ram a farmer, managed to grow shaped-watermelons inside glass cases of different shapes. The shapes he used were: a perfect cube, hemi-spherical, cuboid, cylindrical along with the normal spherical shaped watermelons. Thickness of the skin was same for all the shapes. Each of the glass cases was so designed that the total volume and the weight of the all the water-melons would be equal irrespective of the shape.
A customer wants to buy water-melon for making juice, for which the skin of the water-melon has to be peeled off, and therefore is a waste. Which shape should the customer buy?
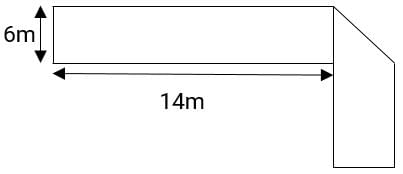
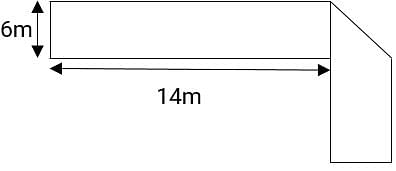
The figure below has been obtained by folding a rectangle. The total area of the figure (as visible) is 144 square meters. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?
A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re-cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?
A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq. ft. Find the lowest possible cost to construct 50% of the total road.
|
56 videos|104 docs|95 tests
|
|
56 videos|104 docs|95 tests
|


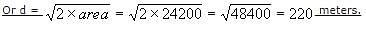
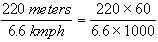 (converting 1 km = 1000 meters and 1 hour = 60 minutes).
(converting 1 km = 1000 meters and 1 hour = 60 minutes).
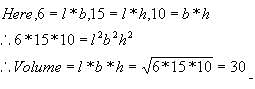
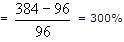
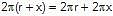

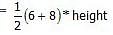
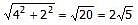
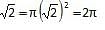
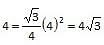
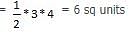
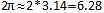 6.28 sq units
6.28 sq units