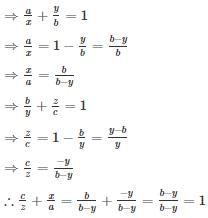Practice Test: Quantitative Aptitude - 1 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 and Tier 2 Mock Test Series 2026 - Practice Test: Quantitative Aptitude - 1
A and B can do a piece of work for Rs.800. A alone can do it in 8 days while B alone can do it in 12 days. With help of C, they finish it in 4 days. Find the ratio of share of B and C.
The curved surface area of a cylindrical pillar is 368 m2 and its volume 1104 m3. Find the height of the cylinder?
A wholesaler mixes 23 kg of rice at Rs. 24 per kg with 27 kg of rice of other variety at Rs. 37 per kg and sells the mixture at Rs. 35 per kg. His profit percent is
When 30% is lost in grinding, a country can export 60 lakh tons of wheat with some of the wheat still remaining. On the other hand if only 20% is lost in grinding, it can export 80 lakh tons of wheat with the same amount of the wheat remaining, then the production of wheat in the country is
A train of length 350 m crosses a bridge of length 250 m in 30 seconds. What is speed of the train?
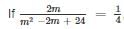 Then the least possible value of m which is a root of the quadratic equation is
Then the least possible value of m which is a root of the quadratic equation is
If α, β are the roots of the equation 2x2 - 3x + 2 = 0, form the equation whose roots are α2, β2 ?
The four triangles formed by joining the pairs of mid points of the sides of a given triangle are congruent if the given triangle is
In the ΔABC, ∠B = 70° and ∠C = 30°, BO and CO are the angle bisectors of ∠ABC and ∠ACB. Find the value of ∠BOC
The area of a trapezium is 441 sq.cm and the ratio of parallel sides is 5 : 9. Also the perpendicular distance between them is 21 cm, the longer of parallel sides is
If cos A = 3/5 and sin B = 5/13, find the value of tan (A + B) is
When a number is divided by 13, the remainder is 11. When the same number is divided by 17, the remainder is 9. What is the number?
A shop keeper sells an article at 20% loss. If he sells it for 100 more, he would earn a profit of 10%.The cost price is
Average of 100 numbers is 50. If the two numbers 60 and 80 are discarded, then find the average of the remaining numbers ?
The difference between simple interest received from two different sources for Rs.13,000 for 2 years is Rs. 65. Then the difference between their rates of interest?
If a – b = 3 and a2 + b2 = 29, find the value of a + b ?
In ∆ABC, AB = 12 cm, BC = 10 cm and AC = 6 cm. Find the approximate length of the median from vertex A.
Two arcs of two different circles are of equal lengths. If these arcs subtend angles of 30° and 60° at the centers of their respective circles, find the ratio of the radii of the two circles.
The area of a square and circle is same and the perimeter of square and equilateral triangle is same, then the ratio between the area of circle and the area of equilateral triangle is
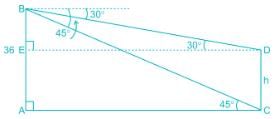
There are two buildings, one on each bank of a river, just opposite to each other. One building is 36 m high. From the top of the this building, the angles of depression of the top and foot of the other building are 30° and 45° respectively. Find the height of the other building?
Directions: The pie - chart shows the percentage of expenditure spend by school on different sports. If the amount of total expenditure is Rs. 5,00,000. Study the diagram and answer the following questions.
Expenditure
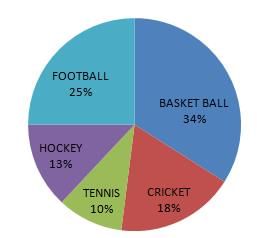
Q. Find the amount of expenditure that is spend on tennis?
Directions: The pie - chart shows the percentage of expenditure spend by school on different sports. If the amount of total expenditure is Rs. 5,00,000. Study the diagram and answer the following questions.
Expenditure

Q. Find the ratio of expenditure that is spend on cricket and hockey?
Directions: The pie - chart shows the percentage of expenditure spend by school on different sports. If the amount of total expenditure is Rs. 5,00,000. Study the diagram and answer the following questions.
Expenditure

Q. How much expenditure more is spent on basketball than football?
Directions: The pie - chart shows the percentage of expenditure spend by school on different sports. If the amount of total expenditure is Rs. 5,00,000. Study the diagram and answer the following questions.
Expenditure

Q. Find the ratio of expenditure on football to the total expenditure?
|
325 docs|152 tests
|



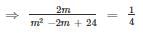
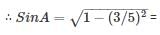 4/5 and tan A = SinA/CosA = 4/3
4/5 and tan A = SinA/CosA = 4/3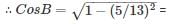 12/13 and tan B = SinB/CosB = 5/12
12/13 and tan B = SinB/CosB = 5/12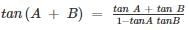
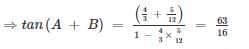
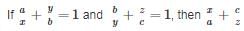 will be equal to
will be equal to