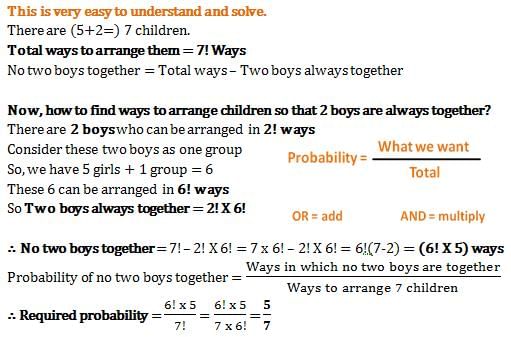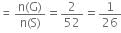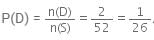Practice Test: Probability - Class 10 MCQ
25 Questions MCQ Test - Practice Test: Probability
If A be the event such that P(A) = 2/5, then P(not A) is equal to
What are the chances that no two boys are sitting together for a photograph if there are 5 girls and 2 boys?
In a single throw of a die, the probability of getting a multiple of 3 is
Find the probability of getting a number greater than 2 when a die is thrown
If a die is rolled, the probability of getting a number between 1 and 6 is
What are the chances that all boys are sitting together for a photograph if there are 5 girls and 3 boys?
What is the probability of getting one head and one tail when a coin is tossed 2 times?
What is the probability of getting two heads when a coin is tossed twice?
What is the probability of getting no head when two coins are tossed?
In a simultaneous throw of two coins the probability of getting at least one head is
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is :
The probability of getting a '10' of black suit is
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is :
The probability of getting a red and a king card is
A bag contains 4 red balls and 3 green balls. A ball is drawn at random. The probability of drawing a green ball is
Which one of the following cannot be the probability of an event
Which one of the following cannot be the probability of an event
If P(E1) = 1/6, P (E2) = 1/3 , P (E3) = 1/6 , where E1, E2, E3 and E4 are elementary events of a random experiment, then P (E4) is equal to
Cards each marked with one of the numbers 4, 5, 6,...., 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Then, the probability of getting an even prime number is
A bag contains 5 red and 4 black balls. A ball is drawn at random from the bag. Then, the probability of getting a black ball is
Find the probability of getting a head in a throw of a coin.
Two fair coins are tossed simultaneously. Find the probability of Getting only one head
Two fair coins are tossed simultaneously. Find the probability of Getting atleast one head