Test: Introduction to Quadratic Equations - Grade 9 MCQ
30 Questions MCQ Test - Test: Introduction to Quadratic Equations
Write the general form of a quadratic polynomia
One of the roots of the quadratic equation 6x2 – x – 2 = 0 is:
Which of the following statement is TRUE?
If n is a non negative integer, then anx n +…+ a 1 x + a0 is a
The two positive numbers differ by 5 and square of their sum is 169 are
If 4 is a root of the equation x2 + 3x + k = 0, then k is
If 8 is a root of the equation x2 – 10x + k = 0, then the value of k is:
Which of following is not a quadratic equation:
Which of the following equations has 2 as a root?
Which of the following equations has the sum of its roots as 3?
Which of the following is not a quadratic equation:
If x = -2 is a root of equation x2 – 4x + K = 0 then value of K is
The same value of x satisfies the equations 4x + 5 = 0 and 4x2 + (5 + 3p)x + 3p2 = 0, then p is
If x = 1 is a root of equation x2 – Kx + 5 = 0 then value of K is
The equation in standard form ax2 + bx + c = 0 is written as :
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
If x = 2 is a root of equation x2 + 3x – k = 0 then value of k is
The condition for equation ax2 + bx + c = 0 to be quadratic is
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____
The equation 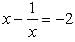 in standard form ax2 + bx + c = 0 is written as
in standard form ax2 + bx + c = 0 is written as
Zeroes of the quadratic polynomial ax2 + bx + c and roots of the quadratic equation ax2 + bx + c = 0 are ——–
The condition for equation ax2 + bx + c = 0 to be linear is
If x2 + 2 kx + 4 = 0 has a root x = 2, then the value of k is?
The value/s of x when (x – 4) (3x + 2) = 0 ________




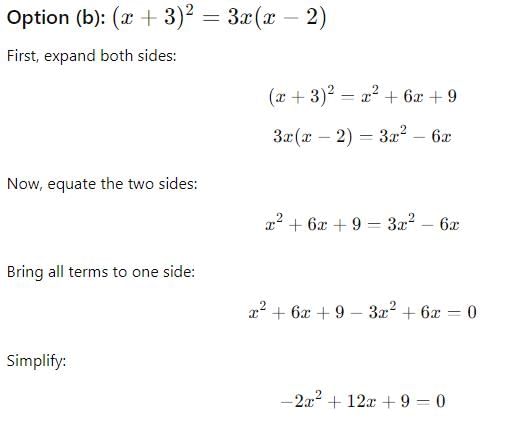

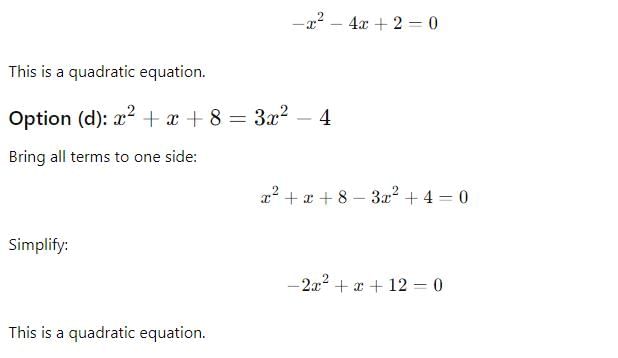



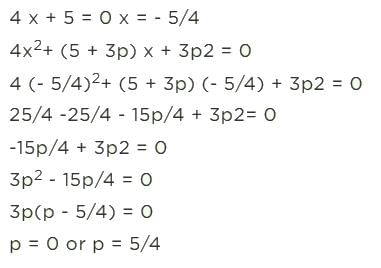
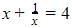
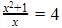

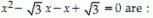
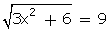 is
is











