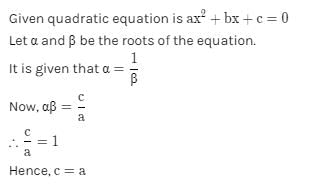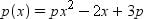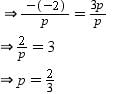Test: Zeroes & Coefficients - Class 9 MCQ
20 Questions MCQ Test Advance Learner Course: Mathematics (Maths) Class 9 - Test: Zeroes & Coefficients
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:
If one zero of polynomial f(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of the other, then k =
Find the quadratic polynomial whose zeros are 2 and -6
If α, β, γ be the zeros of the polynomial p(x) such that α + β + γ = 3, αβ + βγ + γα = -10 and αβγ = -24, then p(x) is
If -√5 and √5 are the roots of the quadratic polynomial. Find the quadratic polynomial.
If one root of polynomial equation ax2 + bx + c = 0 be reciprocal of other, then
If one zero of the polynomial x2 + kx + 18 is double the other zero then k = ?
If one zero of 2x2 – 3x + k is reciprocal to the other, then the value of k is :
Sum and the product of zeroes of the polynomial x2 +7x +10 is
If sum of the zeroes of the polynomial is 4 and their product is 4, then the quadratic polynomial is
What value/s can x take in the expression k(x – 10) (x + 10) = 0 where k is any real number.
Find the sum and the product of zeroes of the polynomial x2 +7x +10
The sum and product of zeros of a quadratic polynomial are 2 and -15 respectively. The quadratic polynomial is
If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 – 4x + 9 is 3, then its third zero is
If α, β are zeroes of the polynomial f(x) = x2 + 5x + 8, then value of (α + β) is
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.
If α , β are the zeroes of f(x) = px2 – 2x + 3p and α + β = αβ then the value of p is:
If the two zeroes of the quadratic polynomial 7x2 – 15x – k are reciprocals of each other, the value of k is:
Find the sum and the product of the zeroes of the polynomial: x2-3x-10
|
13 videos|79 docs|29 tests
|
|
13 videos|79 docs|29 tests
|




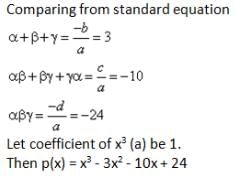
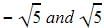 as the roots which means x +
as the roots which means x + 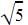 and x-
and x- 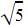 are the factors of the quadratic equation. Multiplying x+
are the factors of the quadratic equation. Multiplying x+ 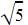 and x-
and x- 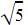 and applying a2-b2 we get the equation x2-5.
and applying a2-b2 we get the equation x2-5.