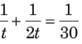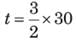CAT Previous Year Questions: Time & Work - CAT MCQ
20 Questions MCQ Test - CAT Previous Year Questions: Time & Work
Rahul, Rakshita and Gurmeet, working together, would have taken more than 7 days to finish a job. On the other hand, Rahul and Gurmeet, working together would have taken less than 15 days to finish the job. However, they all worked together for 6 days, followed by Rakshita, who worked alone for 3 more days to finish the job. If Rakshita had worked alone on the job then the number of days she would have taken to finish the job, cannot be
[2023]
Gautam and Suhani, working together, can finish a job in 20 days. If Gautam does only 60% of his usual work on a day, Suhani must do 150% of her usual work on that day to exactly make up for it. Then, the number of days required by the faster worker to complete the job working alone is
[2023]
The amount of job that Amal, Sunil and Kamal can individually do in a day, are in harmonic progression. Kamal takes twice as much time as Amal to do the same amount of job. If Amal and Sunil work for 4 days and 9 days, respectively, Kamal needs to work for 16 days to finish the remaining job. Then the number of days Sunil will take to finish the job working alone, is
[2023]
When they work alone, B needs 25% more time to finish a job than A does. They two finish the job in 13 days in the following manner: A works alone till half the job is done, then A and B work together for four days, and finally B works alone to complete the remaining 5% of the job. In how many days can B alone finish the entire job?
Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job, If Bimal has done 10% of the job, then in how many days was the job done?
(CAT 2019)
A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on ?
(CAT 2018)
Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it?
(CAT 2018)
Rima can do a work in 1 day and Bhavik can do the same work in 20 hours. In how much time they will finish the work together?
A tank is emptied everyday at a fixed time point, Immediately thereafter, either pump A or pump B or both start working until the tank is full. On Monday, A alone completed filling the tank at 8 pm. On Tuesday, B alone completed filling the tank at 6 pm. On Wednesday, A alone worked till 5 pm, and then B worked alone from 5 pm to 7 pm, to fill the tank. At what time was the tank filled on Thursday if both pumps were used simultaneously all along?
(CAT 2018)
A water tank has inlets of two types A and B. All inlets of type A when open, bring in water at the same rate. All inlets of type B, when open, bring in water at the same rate. The empty tank is completely filled in 30 minutes if 10 inlets of type A and 45 inlets of type B are open, and in 1 hour if 8 inlets of type A and 18 inlets of type B are open. In how many minutes will the empty tank get completely filled if 7 inlets of type A and 27 inlets of type B are open ?
(CAT 2018)
Ramesh and Ganesh can together complete a work in 16 days. After seven days of working together, Ramesh got sick and his efficiency fell by 30%. As a result, they completed the work in 17 days instead of 16 days. If Ganesh had worked alone after Ramesh got sick, in how many days would he have completed the remaining work?
(CAT 2018)
A person can complete a job in 120 days. He works alone on Day 1. On Day 2, he is joined by another person who also can complete the job in exactly 120 days. On Day 3, they are joined by another person of equal efficiency. Like this, everyday a new person with the same efficiency joins the work. How many days are required to complete the job?
(CAT 2017)
A tank has an inlet pipe and an outlet pipe. If the outlet pipe is closed, then the inlet pipe fills the empty tank in 8 hours. If the outlet pipe is open, then the inlet pipe fills the empty tank in 10 hours. If only the outlet pipe is open, then in how many hours the full tank becomes half-full?
(CAT 2017)
Amal can complete a job in 10 days and Bimal can complete it in 8 days. Amal, Bimal and Kamal together complete the job in 4 days and are paid a total amount of Rs. 1000 as remuneration. If this amount is shared by them in proportion to their work, then Kamal's share, in rupees, is
(CAT 2017)
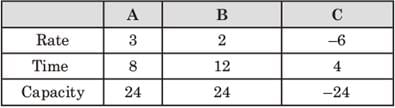
Four two-way pipes, A,B,C and D can either fill an empty tank or drain the full tank in 4, 10, 12 and 20 minutes, respectively. All four pipes were opened simultaneously when the tank is empty. Under which of the following conditions, the tank would be half filled after 30 minutes?
(XAT 2017)
A water tank has M inlet pipes and N outlet pipes. An inlet pipe can fill the tank in 8 hours while an outlet pipe can empty the full tank in 12 hours. If all pipes are left open simultaneously, it takes 6 hours to fill the empty tank. What is the relationship between M and N?
(XAT 2016)
In the marketing management course of an MBA programme, you and your roommate can complete an assignment in 30 days. If you are twice as efficient as your roommate, the time required by each to complete the assignment individually is
(IIFT 2016)
Three pipes are connected to an inverted cone, with its base at the top. Two inlet pipes, A and B, are connected to the top of the cone and can fill the empty cone in 8 hours and 12 hours, respectively. The outlet pipe C, connected to the bottom, can empty a filled cone in 4 hours. When the cone is completely filled with water, all three pipes are opened. Two of the three pipes remain open for 20 hours continuously and the third pipe remains open for a lesser time. As a result, the height of the water inside the cone comes down to 50%. Which of the following options would be possible?
(XAT 2015)
A tank is connected with both inlet pipes and outlet pipes. Individually, an inlet pipe can fill the tank in 7 hours and an outlet pipe can empty it in 5 hours. If all the pipes are kept open, it takes exactly 7 hours for a completely filled-in tank to empty. If the total number of pipes connected to the tank is 11, how many of these are inlet pipes?
(IIFT 2015)
Three carpenters P,Q and R are entrusted with office furniture work. P can do a job in 42 days. If Q is 26% more efficient than P, and R is 50% more efficient than Q, then Q and R together can finish the job in approximately :
(IIFT 2015)