Sample Test: LR & DI- 2 - CAT MCQ
20 Questions MCQ Test - Sample Test: LR & DI- 2
Directions: Study the given information and answer the following question.
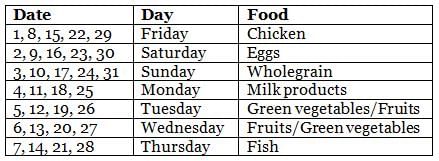
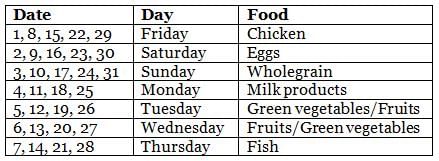
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(1) On 8th May, Sean did not eat fish, while on 23rd May, Sean ate eggs only.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Q. On which of the following days of the week did Sean eat wholegrain only?
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Directions: Study the given information and answer the following question.
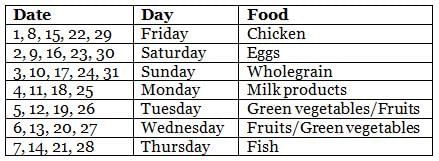
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(1) On 8th May, Sean did not eat fish, while on 23rd May, Sean ate eggs only.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Q. On which of the following days did Sean eat milk products only?
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Directions: Study the given information and answer the following question.
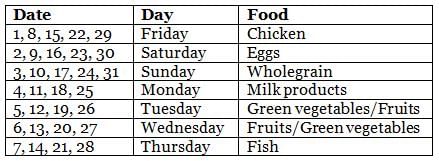
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(1) On 8th May, Sean did not eat fish, while on 23rd May, Sean ate eggs only.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Q. Which of the following food items did Sean eat for the most number of days?
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Directions: Study the given information and answer the following question.
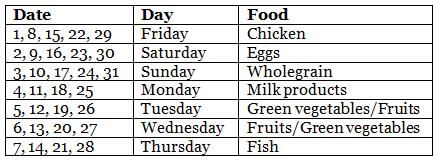
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(1) On 8th May, Sean did not eat fish, while on 23rd May, Sean ate eggs only.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Q. Which of the following statements is definitely true?
Directions: Study the given information and answer the following question.
Sean's dietitian prepared a diet chat for him for the month of May, which had seven different types of food to be consumed during different days. Types of food included chicken, fish, eggs, green vegetables, wholegrain, milk products, and fruits. Further, on a particular day of the week throughout the month, he ate the same type of food. For example, on all Mondays, he ate the same type of food, and so on for all days of the week. Further, the following information is known about the type of food he ate on some days of May.
(1) On 8th May, Sean did not eat fish, while on 23rd May, Sean ate eggs only.
(2) On Mondays, Sean ate neither fish nor wholegrain and on 17th May, Sean ate wholegrain.
(3) There were at least 2 days between the day he ate fish only and the day he ate milk products only.
(4) There were five Saturdays and five Sundays in that May.
(5) He ate green vegetables only and fruits only on two consecutive days, but he ate neither of these on Thursday.
Q. Which two types of food were consumed by Sean on two consecutive days?
Directions: Study the given information and answer the following question.
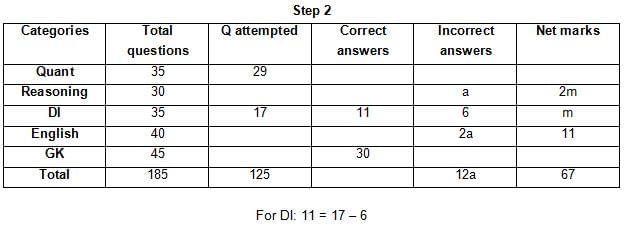
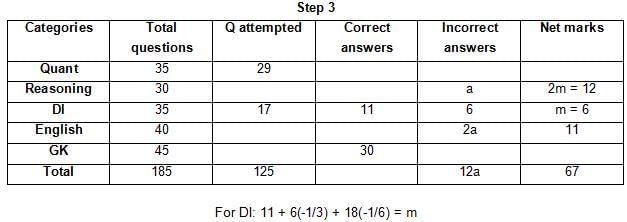
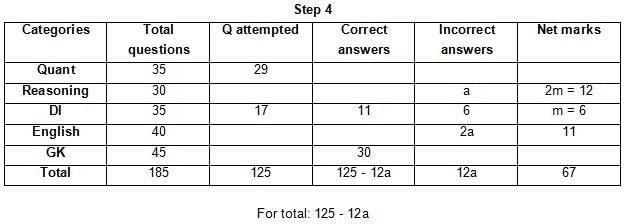
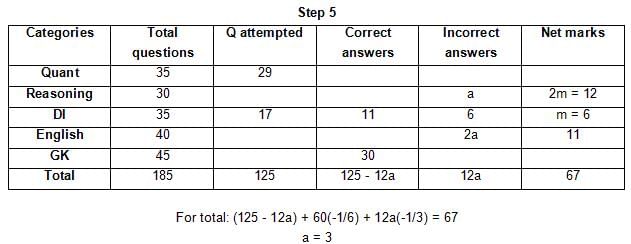
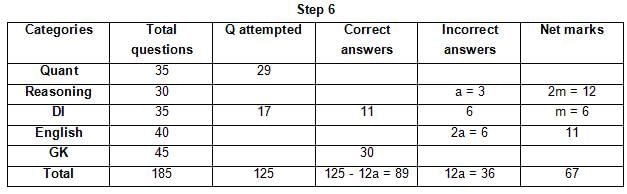
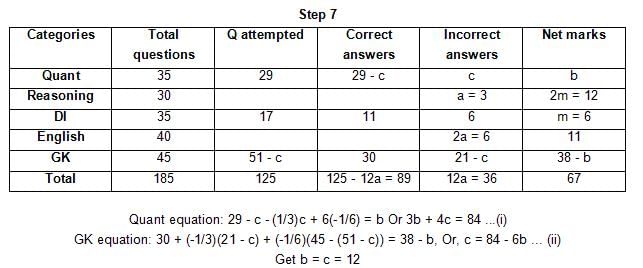
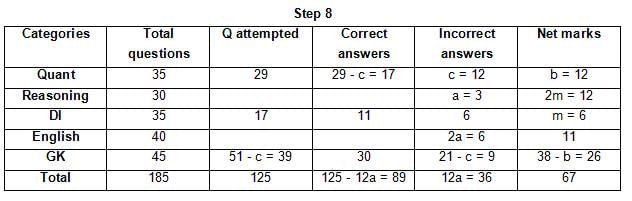
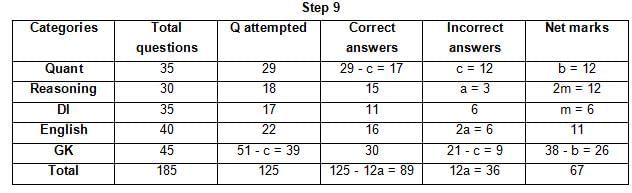
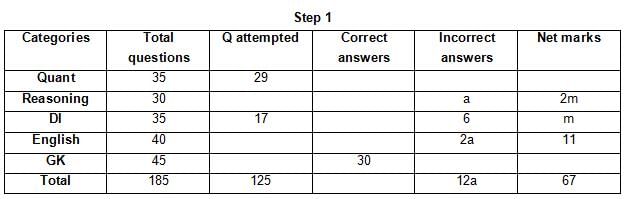
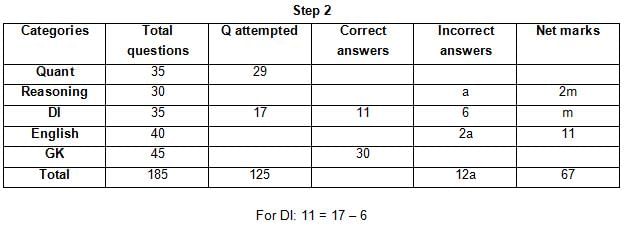
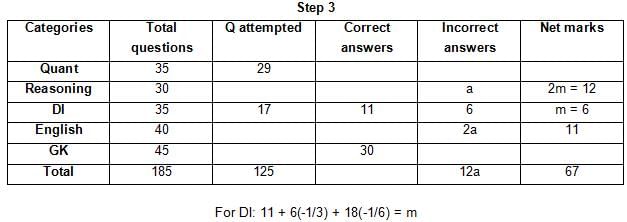
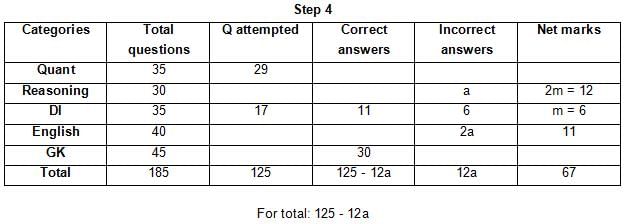
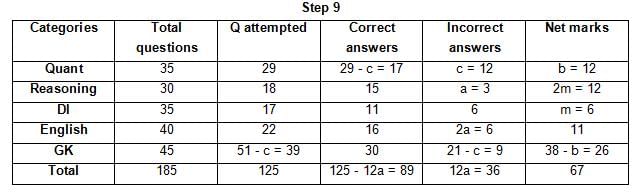
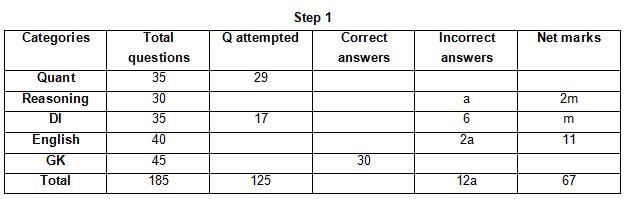
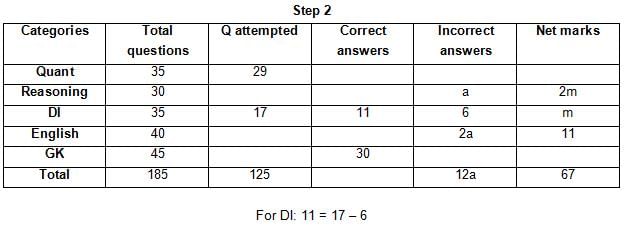
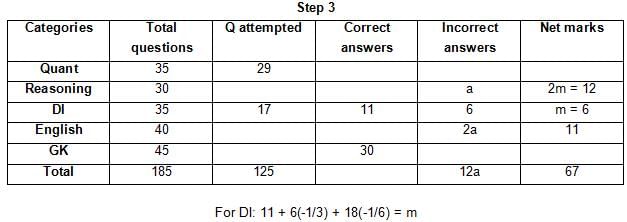
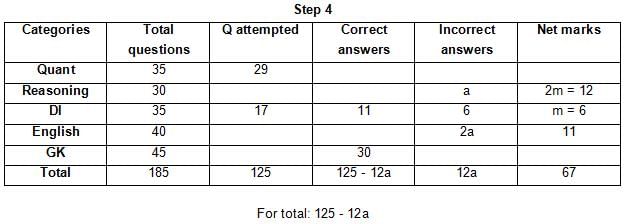
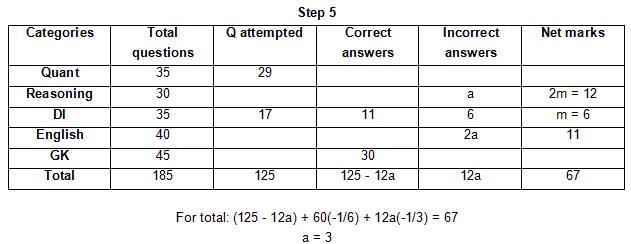
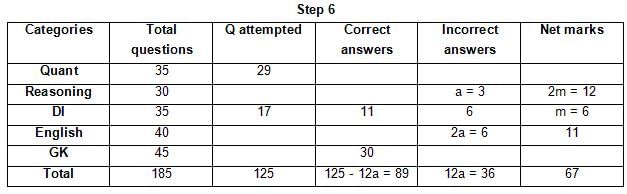
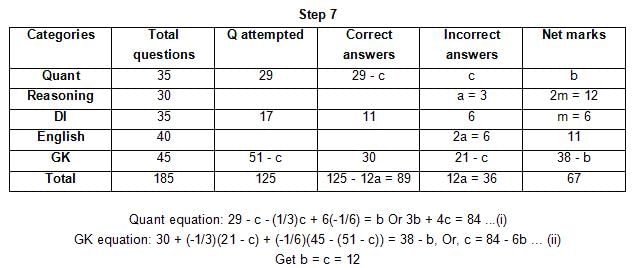
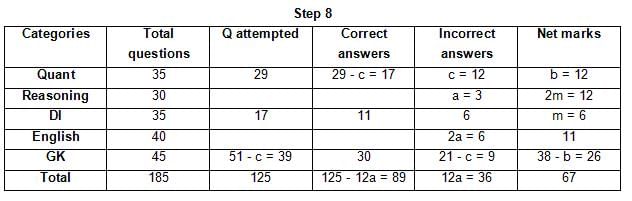
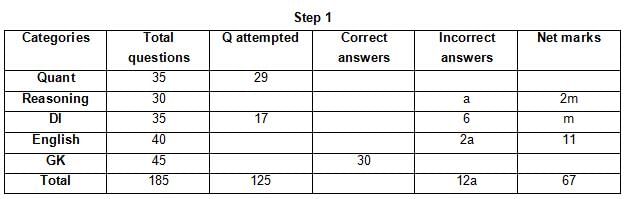
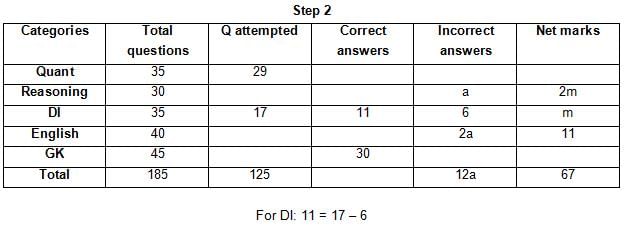
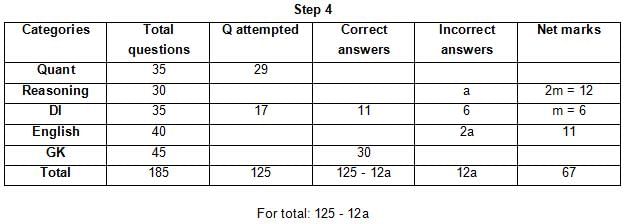
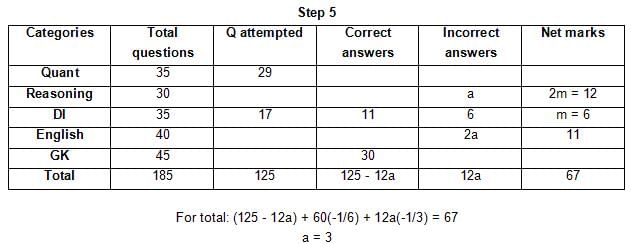
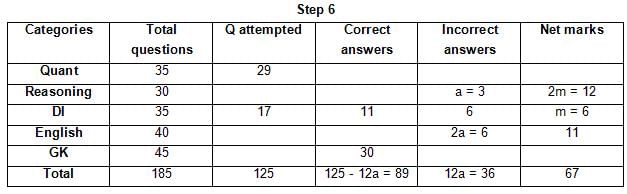
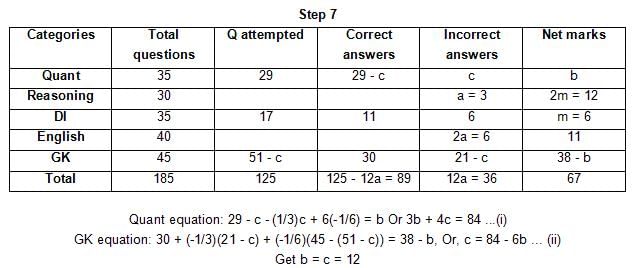
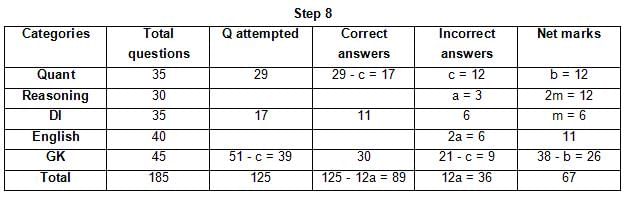
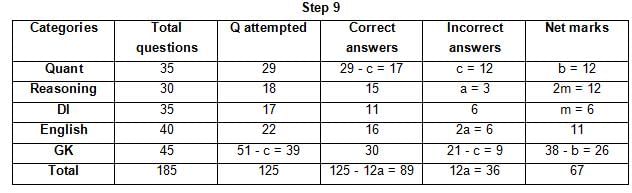
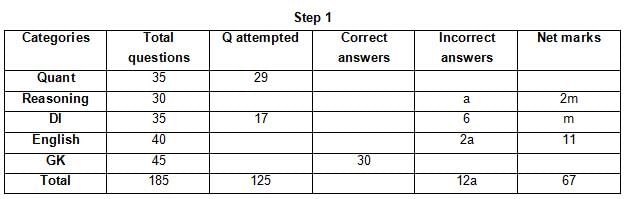
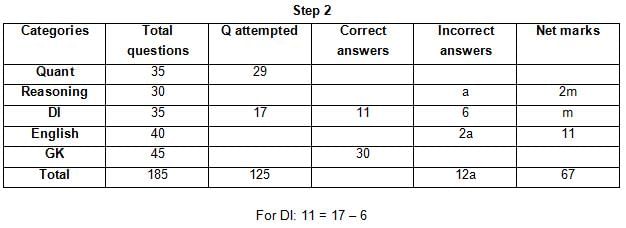
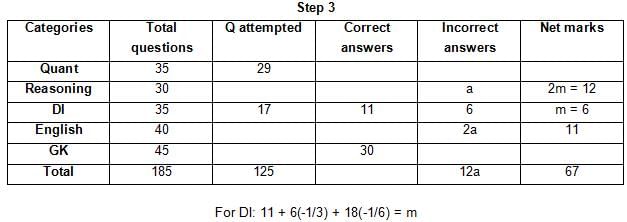
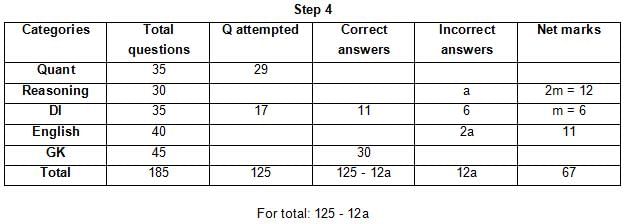
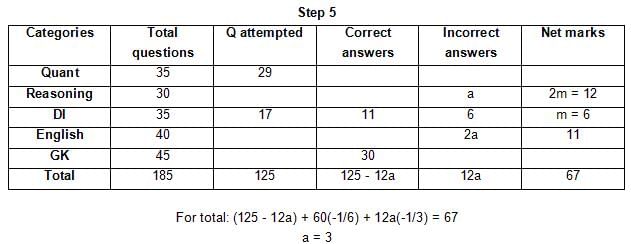
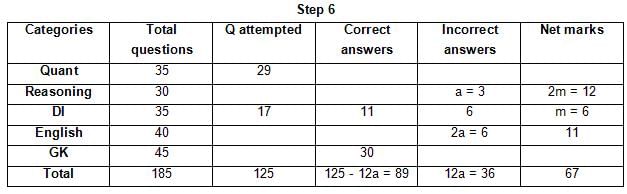
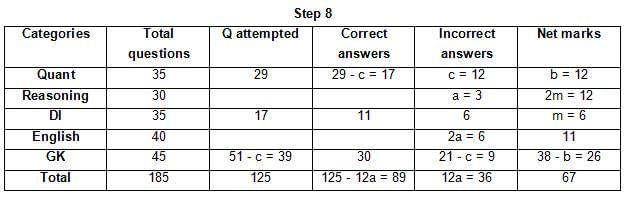
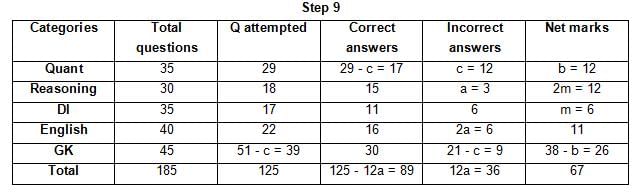
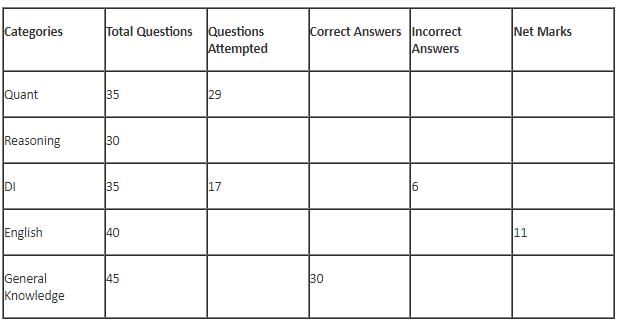
The table below gives some information about marks scored by Joey in a written exam for University Professor, which consists of five main categories: Quant, Reasoning, DI, English, and General Knowledge
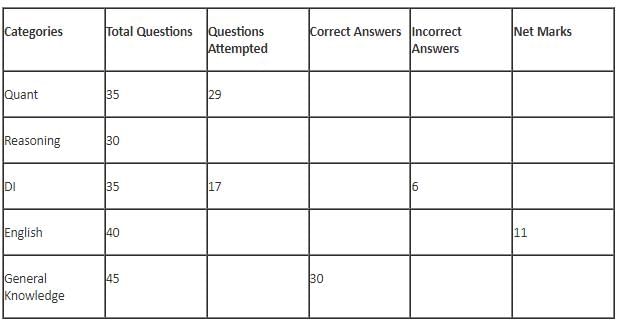
The following data is also provided:
(1) For every correct answer, the candidate gets one mark, for every un-attempted question, the candidate loses 1/6 of a mark, and for every incorrect answer, the student loses 1/3 of a mark.
(2) Joey scores 67 marks and he attempts 125 questions.
(3) The number of incorrect answers given by Joey in English is 1/6 of total number of incorrect answers and twice the number of incorrect answers in Reasoning.
(4) Joey's net marks in Reasoning are double than those in DI.
Q. Key in the total number of incorrect answers given by Jeoy in Reasoning.
Directions: Study the given information and answer the following question.
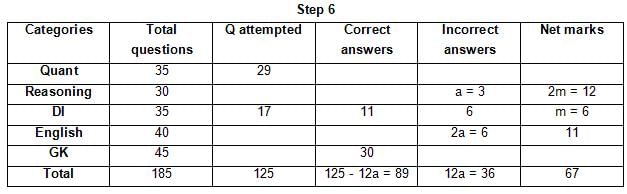
The table below gives some information about marks scored by Joey in a written exam for University Professor, which consists of five main categories: Quant, Reasoning, DI, English, and General Knowledge
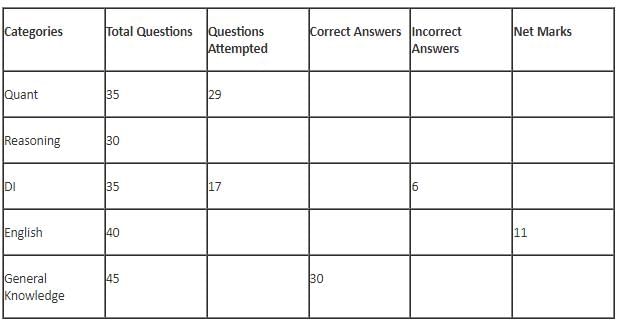
The following data is also provided:
(1) For every correct answer, the candidate gets one mark, for every un-attempted question, the candidate loses 1/6 of a mark, and for every incorrect answer, the student loses 1/3 of a mark.
(2) Joey scores 67 marks and he attempts 125 questions.
(3) The number of incorrect answers given by Joey in English is 1/6 of total number of incorrect answers and twice the number of incorrect answers in Reasoning.
(4) Joey's net marks in Reasoning are double than those in DI.
Q. The highest number of incorrect answers given by Joey in any category is ____.
Directions: Study the given information and answer the following question.
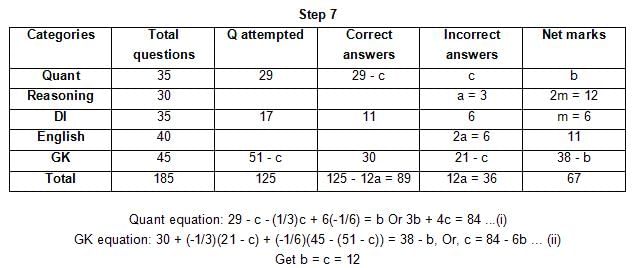
The table below gives some information about marks scored by Joey in a written exam for University Professor, which consists of five main categories: Quant, Reasoning, DI, English, and General Knowledge
The following data is also provided:
(1) For every correct answer, the candidate gets one mark, for every un-attempted question, the candidate loses 1/6 of a mark, and for every incorrect answer, the student loses 1/3 of a mark.
(2) Joey scores 67 marks and he attempts 125 questions.
(3) The number of incorrect answers given by Joey in English is 1/6 of total number of incorrect answers and twice the number of incorrect answers in Reasoning.
(4) Joey's net marks in Reasoning are double than those in DI.
Q. Key in the number of questions attempted by Joey in Reasoning.
Directions: Study the given information and answer the following question.
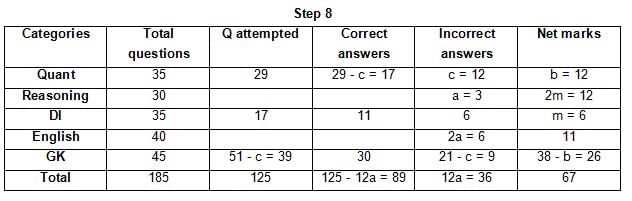
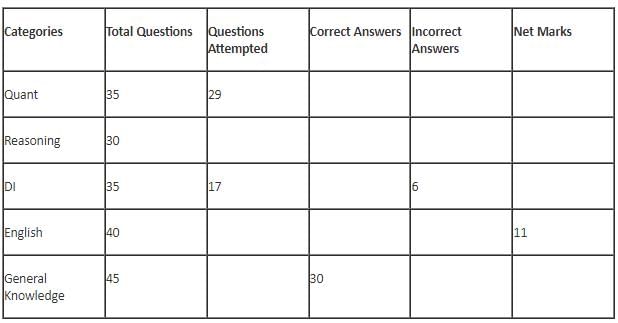
The table below gives some information about marks scored by Joey in a written exam for University Professor, which consists of five main categories: Quant, Reasoning, DI, English, and General Knowledge
The following data is also provided:
(1) For every correct answer, the candidate gets one mark, for every un-attempted question, the candidate loses 1/6 of a mark, and for every incorrect answer, the student loses 1/3 of a mark.
(2) Joey scores 67 marks and he attempts 125 questions.
(3) The number of incorrect answers given by Joey in English is 1/6 of total number of incorrect answers and twice the number of incorrect answers in Reasoning.
(4) Joey's net marks in Reasoning are double than those in DI.
Q. What is the percentage accuracy of Joey in the examination?
Directions: Study the given information and answer the following question.
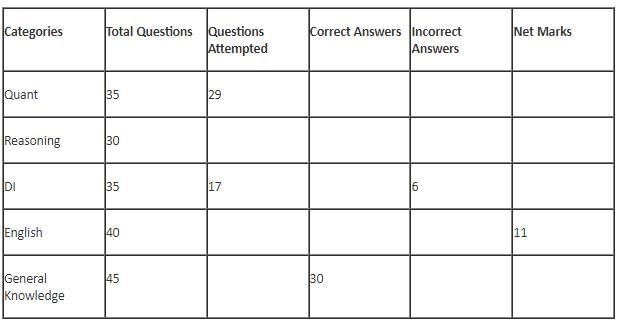
The table below gives some information about marks scored by Joey in a written exam for University Professor, which consists of five main categories: Quant, Reasoning, DI, English, and General Knowledge
The following data is also provided:
(1) For every correct answer, the candidate gets one mark, for every un-attempted question, the candidate loses 1/6 of a mark, and for every incorrect answer, the student loses 1/3 of a mark.
(2) Joey scores 67 marks and he attempts 125 questions.
(3) The number of incorrect answers given by Joey in English is 1/6 of total number of incorrect answers and twice the number of incorrect answers in Reasoning.
(4) Joey's net marks in Reasoning are double than those in DI.
Q. What is the ratio of the number of questions attempted to the number of incorrect answers?
Directions: Read the given information carefully and answer the question that follows.
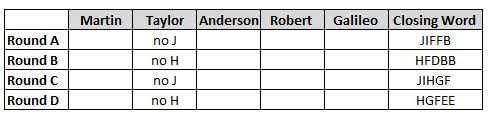
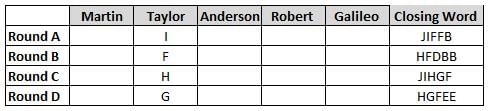
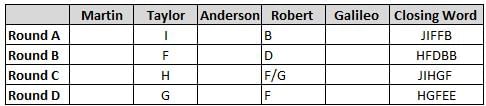
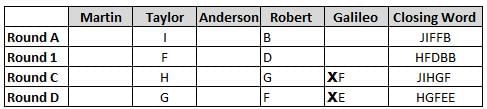
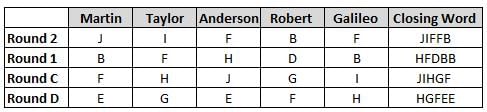
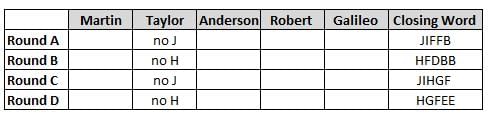
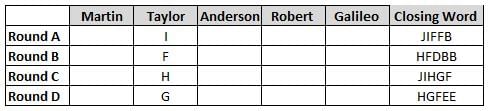
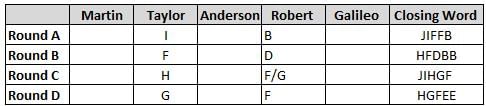
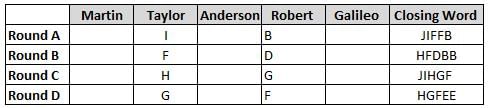
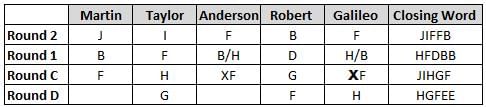
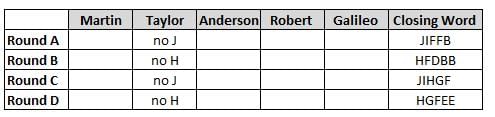
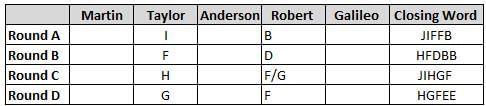
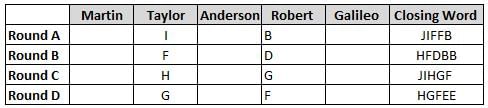
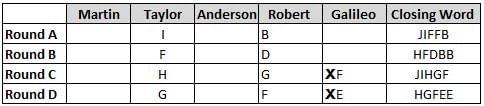
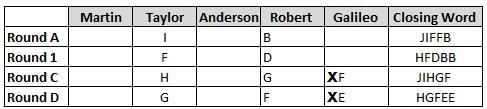
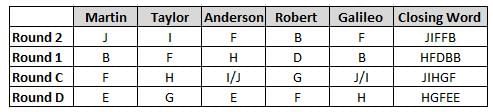
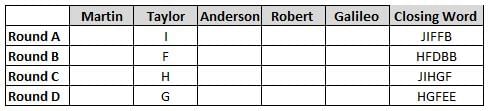
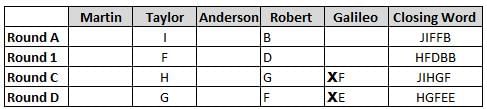
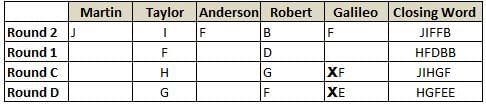
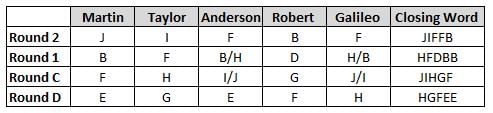
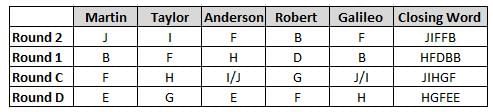
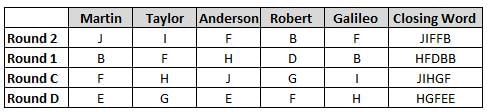
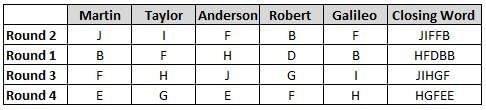
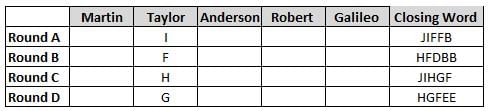
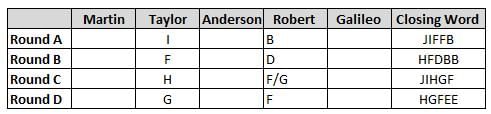
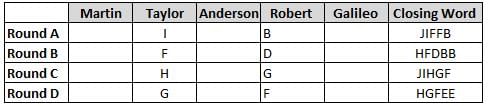
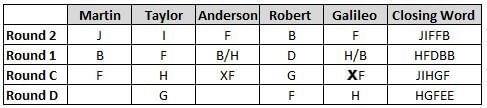
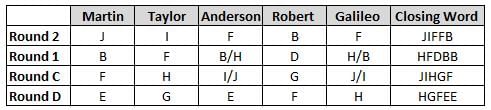
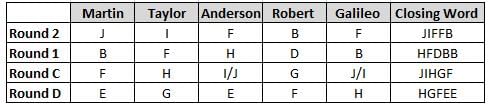
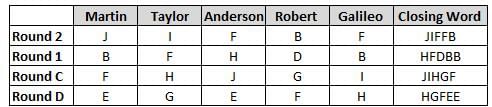
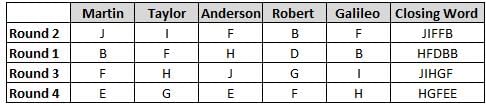
Martin, Taylor, Anderson, Robert and Galileo are playing a card game. Each card bears a letter from A to J on it. In each round of the game, each person independently picks a card and after each of the five persons have picked one card, the five cards are placed in descending alphabetical order of the letters on them such that the card with the letter that appears first in alphabetical order is placed at the end (extreme right) and the card with a letter that appears later in alphabetical order is placed next to the first to the left. In this way, all cards of a round are placed together. The word, so formed, in each round, is labeled as the closing word of that round. After exactly four rounds, the person who picks the leftmost letter of the closing word across the four rounds is declared the winner of the game. No person can pick the same letter in any two rounds.
The closing words of each round are JIFFB, HFDBB, JIHGF and HGFEE, in any order.
It is also known that
(1) Taylor picked cards with consecutive letters across the four rounds, but not necessarily in any order and in none of the rounds did the letter of a card that he picked become the leftmost letter of the closing word
(2) in each round, the letter of the card that Taylor picked was higher in alphabetical order than the one that Robert picked, while in the second round, Anderson and Galileo picked the same lettered cards
(3) the person who was declared the winner picked the card with a letter that appeared earlier in alphabetical order of the closing word in only one round, which was the third round
(4) for only one person is the difference between the highest lettered card that he picked and the lowest lettered card that he picked was 8 according to the numerical value of letter (assigned in ascending order from A to Z, beginning 1 to 26) and this person picked his least lettered card in the first round
(5) no one picked the same lettered card as Robert did in any round and Robert and Galileo did not pick cards with consecutive letters in any round
Q. Who was the winner of the game?
Directions: Read the given information carefully and answer the question that follows.
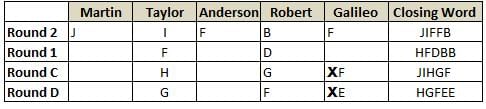
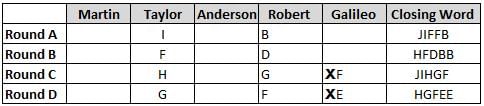
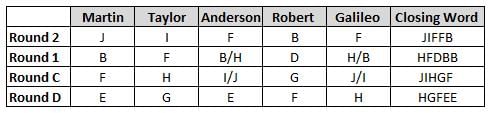
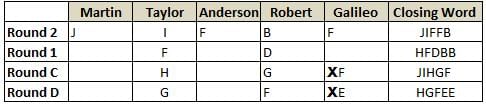
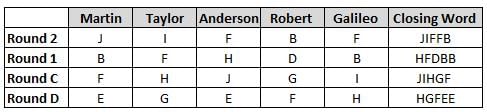
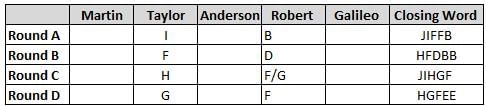
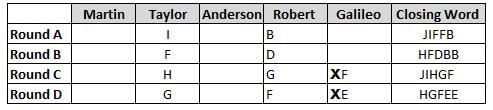
Martin, Taylor, Anderson, Robert and Galileo are playing a card game. Each card bears a letter from A to J on it. In each round of the game, each person independently picks a card and after each of the five persons have picked one card, the five cards are placed in descending alphabetical order of the letters on them such that the card with the letter that appears first in alphabetical order is placed at the end (extreme right) and the card with a letter that appears later in alphabetical order is placed next to the first to the left. In this way, all cards of a round are placed together. The word, so formed, in each round, is labeled as the closing word of that round. After exactly four rounds, the person who picks the leftmost letter of the closing word across the four rounds is declared the winner of the game. No person can pick the same letter in any two rounds.
The closing words of each round are JIFFB, HFDBB, JIHGF and HGFEE, in any order.
It is also known that
(1) Taylor picked cards with consecutive letters across the four rounds, but not necessarily in any order and in none of the rounds did the letter of a card that he picked become the leftmost letter of the closing word
(2) in each round, the letter of the card that Taylor picked was higher in alphabetical order than the one that Robert picked, while in the second round, Anderson and Galileo picked the same lettered cards
(3) the person who was declared the winner picked the card with a letter that appeared earlier in alphabetical order of the closing word in only one round, which was the third round
(4) for only one person is the difference between the highest lettered card that he picked and the lowest lettered card that he picked was 8 according to the numerical value of letter (assigned in ascending order from A to Z, beginning 1 to 26) and this person picked his least lettered card in the first round
(5) no one picked the same lettered card as Robert did in any round and Robert and Galileo did not pick cards with consecutive letters in any round
Q. Which of the following letters did Anderson pick in the first round?
Directions: Read the given information carefully and answer the question that follows.
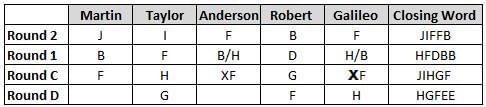
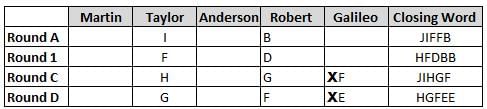
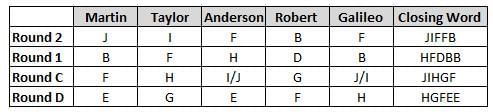
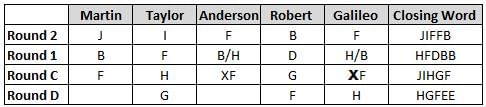
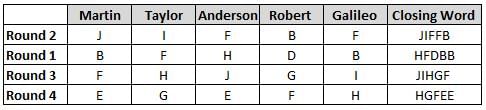
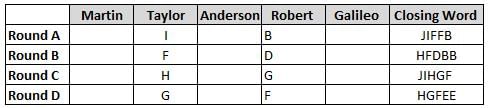
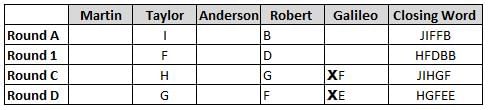
Martin, Taylor, Anderson, Robert and Galileo are playing a card game. Each card bears a letter from A to J on it. In each round of the game, each person independently picks a card and after each of the five persons have picked one card, the five cards are placed in descending alphabetical order of the letters on them such that the card with the letter that appears first in alphabetical order is placed at the end (extreme right) and the card with a letter that appears later in alphabetical order is placed next to the first to the left. In this way, all cards of a round are placed together. The word, so formed, in each round, is labeled as the closing word of that round. After exactly four rounds, the person who picks the leftmost letter of the closing word across the four rounds is declared the winner of the game. No person can pick the same letter in any two rounds.
The closing words of each round are JIFFB, HFDBB, JIHGF and HGFEE, in any order.
It is also known that
(1) Taylor picked cards with consecutive letters across the four rounds, but not necessarily in any order and in none of the rounds did the letter of a card that he picked become the leftmost letter of the closing word
(2) in each round, the letter of the card that Taylor picked was higher in alphabetical order than the one that Robert picked, while in the second round, Anderson and Galileo picked the same lettered cards
(3) the person who was declared the winner picked the card with a letter that appeared earlier in alphabetical order of the closing word in only one round, which was the third round
(4) for only one person is the difference between the highest lettered card that he picked and the lowest lettered card that he picked was 8 according to the numerical value of letter (assigned in ascending order from A to Z, beginning 1 to 26) and this person picked his least lettered card in the first round
(5) no one picked the same lettered card as Robert did in any round and Robert and Galileo did not pick cards with consecutive letters in any round
Q. Who picked the least ranked alphabet according to alphabetical order in the fourth round?
Directions: Read the given information carefully and answer the question that follows.
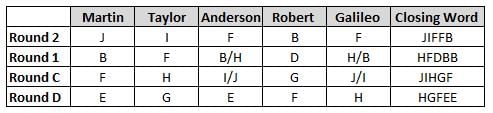
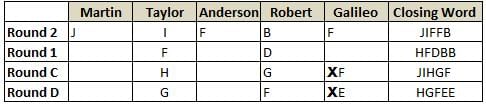
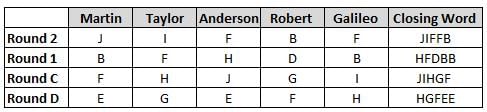
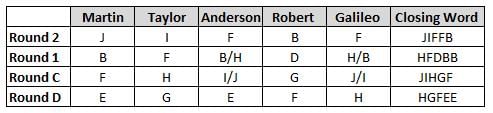
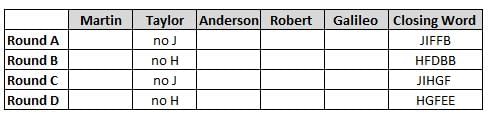
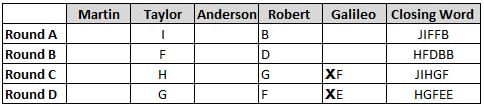
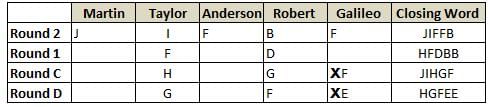
Martin, Taylor, Anderson, Robert and Galileo are playing a card game. Each card bears a letter from A to J on it. In each round of the game, each person independently picks a card and after each of the five persons have picked one card, the five cards are placed in descending alphabetical order of the letters on them such that the card with the letter that appears first in alphabetical order is placed at the end (extreme right) and the card with a letter that appears later in alphabetical order is placed next to the first to the left. In this way, all cards of a round are placed together. The word, so formed, in each round, is labeled as the closing word of that round. After exactly four rounds, the person who picks the leftmost letter of the closing word across the four rounds is declared the winner of the game. No person can pick the same letter in any two rounds.
The closing words of each round are JIFFB, HFDBB, JIHGF and HGFEE, in any order.
It is also known that
(1) Taylor picked cards with consecutive letters across the four rounds, but not necessarily in any order and in none of the rounds did the letter of a card that he picked become the leftmost letter of the closing word
(2) in each round, the letter of the card that Taylor picked was higher in alphabetical order than the one that Robert picked, while in the second round, Anderson and Galileo picked the same lettered cards
(3) the person who was declared the winner picked the card with a letter that appeared earlier in alphabetical order of the closing word in only one round, which was the third round
(4) for only one person is the difference between the highest lettered card that he picked and the lowest lettered card that he picked was 8 according to the numerical value of letter (assigned in ascending order from A to Z, beginning 1 to 26) and this person picked his least lettered card in the first round
(5) no one picked the same lettered card as Robert did in any round and Robert and Galileo did not pick cards with consecutive letters in any round
Q. Who among the following picked the highest letter according to alphabetical order in more than one rounds?
Directions: Read the given information carefully and answer the question that follows.
Martin, Taylor, Anderson, Robert and Galileo are playing a card game. Each card bears a letter from A to J on it. In each round of the game, each person independently picks a card and after each of the five persons has picked one card, the five cards are placed in the descending alphabetical order of the letters on them such that the card with the letter that appears first in the alphabetical order is placed at the end (extreme right) and the card with a letter that appears later in the alphabetical order is placed next to the first to the left. In this way, all cards of a round are placed together. The word, so formed, in each round, is labelled as the closing word of that round. After exactly four rounds, the person who picks the leftmost letter of the closing word across the four rounds is declared the winner of the game. No person can pick the same letter in any two rounds.
The closing words of each round are JIFFB, HFDBB, JIHGF and HGFEE, in any order.
It is also known that:
(1) Taylor picked cards with consecutive letters across the four rounds, but not necessarily in any order and in none of the rounds did the letter of a card that he picked become the leftmost letter of the closing word.
(2) In each round, the letter of the card that Taylor picked was higher in the alphabetical order than the one that Robert picked, while in the second round, Anderson and Galileo picked the same lettered cards.
(3) The person who was declared the winner picked the card with a letter that appeared earlier in the alphabetical order of the closing word in only one round, which was the third round.
(4) For only one person is the difference between the highest lettered card that he picked and the lowest lettered card that he picked was 8 according to the numerical value of letter (assigned in ascending order from A to Z, beginning 1 to 26) and this person picked his least lettered card in the first round.
(5) No one picked the same lettered card as Robert did in any round and Robert and Galileo did not pick cards with consecutive letters in any round.
Q. The round in which no vowel got picked was
Directions: Study the given information and answer the following question.
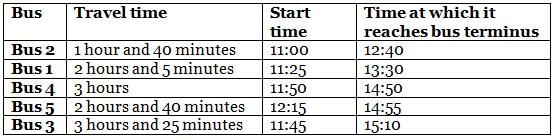
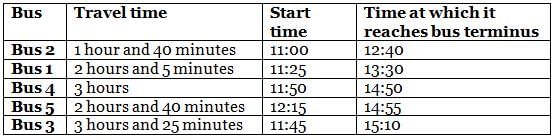
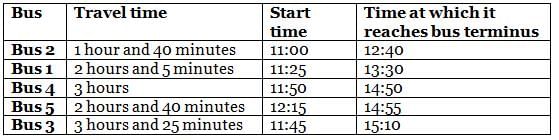
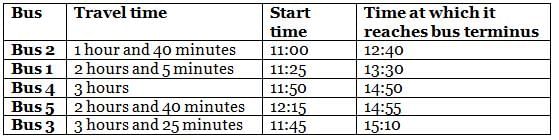
On a particular day, five buses - Bus 1, Bus 2, Bus 3, Bus 4 and Bus 5 - destined for the same bus terminus started from different starting points and travelled for different times: 1 hour and 40 minutes, 2 hours and 5 minutes, 2 hours and 40 minutes, 3 hours, and 3 hours and 25 minutes to reach the bus terminus. The journey of buses started at different times, i.e. 11:00, 11:25, 11:45, 11:50 and 12:15.
It is also known that
(1) no two buses reached the bus terminus at the same time
(2) Bus 1, whose travel time was 2 hours and 5 minutes, did not reach the bus terminus before 13:20
(3) among the five buses, the last bus to reach the bus terminus was Bus 3
(4) Bus 4 reached the bus terminus after 14:45, but the travel time was not 3 hours and 25 minutes
(5) among the five buses, at least three buses reached the bus terminus before Bus 5 did
Q. What was the travel time for the bus that reached the bus terminus before 1:00?
Directions: Study the given information and answer the following question.
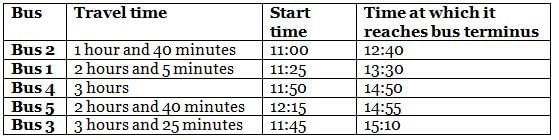
On a particular day, five buses - Bus 1, Bus 2, Bus 3, Bus 4 and Bus 5 - destined for the same bus terminus started from different starting points and travelled for different times: 1 hour and 40 minutes, 2 hours and 5 minutes, 2 hours and 40 minutes, 3 hours, and 3 hours and 25 minutes to reach the bus terminus. The journey of buses started at different times, i.e. 11:00, 11:25, 11:45, 11:50 and 12:15.
It is also known that
(1) no two buses reached the bus terminus at the same time
(2) Bus 1, whose travel time was 2 hours and 5 minutes, did not reach the bus terminus before 13:20
(3) among the five buses, the last bus to reach the bus terminus was Bus 3
(4) Bus 4 reached the bus terminus after 14:45, but the travel time was not 3 hours and 25 minutes
(5) among the five buses, at least three buses reached the bus terminus before Bus 5 did
Q. At what time did Bus 4 reach the terminus?
Directions: Study the given information and answer the following question.
On a particular day, five buses - Bus 1, Bus 2, Bus 3, Bus 4 and Bus 5 - destined for the same bus terminus started from different starting points and travelled for different times: 1 hour and 40 minutes, 2 hours and 5 minutes, 2 hours and 40 minutes, 3 hours, and 3 hours and 25 minutes to reach the bus terminus. The journey of buses started at different times, i.e. 11:00, 11:25, 11:45, 11:50 and 12:15.
It is also known that
(1) no two buses reached the bus terminus at the same time
(2) Bus 1, whose travel time was 2 hours and 5 minutes, did not reach the bus terminus before 13:20
(3) among the five buses, the last bus to reach the bus terminus was Bus 3
(4) Bus 4 reached the bus terminus after 14:45, but the travel time was not 3 hours and 25 minutes
(5) among the five buses, at least three buses reached the bus terminus before Bus 5 did
Q. What was the travel time (in minutes) for the bus that started at 11:45?
Directions: Study the given information and answer the following question.
On a particular day, five buses - Bus 1, Bus 2, Bus 3, Bus 4 and Bus 5 - destined for the same bus terminus started from different starting points and travelled for different times: 1 hour and 40 minutes, 2 hours and 5 minutes, 2 hours and 40 minutes, 3 hours, and 3 hours and 25 minutes to reach the bus terminus. The journey of buses started at different times, i.e. 11:00, 11:25, 11:45, 11:50 and 12:15.
It is also known that
(1) no two buses reached the bus terminus at the same time
(2) Bus 1, whose travel time was 2 hours and 5 minutes, did not reach the bus terminus before 13:20
(3) among the five buses, the last bus to reach the bus terminus was Bus 3
(4) Bus 4 reached the bus terminus after 14:45, but the travel time was not 3 hours and 25 minutes
(5) among the five buses, at least three buses reached the bus terminus before Bus 5 did
Q. Which bus should a person take after 11:30 so that his travel time is minimum?
Directions: Study the given information and answer the following question.
On a particular day, five buses - Bus 1, Bus 2, Bus 3, Bus 4 and Bus 5 - destined for the same bus terminus started from different starting points and travelled for different times: 1 hour and 40 minutes, 2 hours and 5 minutes, 2 hours and 40 minutes, 3 hours, and 3 hours and 25 minutes to reach the bus terminus. The journey of buses started at different times, i.e. 11:00, 11:25, 11:45, 11:50 and 12:15.
It is also known that
(1) no two buses reached the bus terminus at the same time
(2) Bus 1, whose travel time was 2 hours and 5 minutes, did not reach the bus terminus before 13:20
(3) among the five buses, the last bus to reach the bus terminus was Bus 3
(4) Bus 4 reached the bus terminus after 14:45, but the travel time was not 3 hours and 25 minutes
(5) among the five buses, at least three buses reached the bus terminus before Bus 5 did
Q. Which of the following is true?