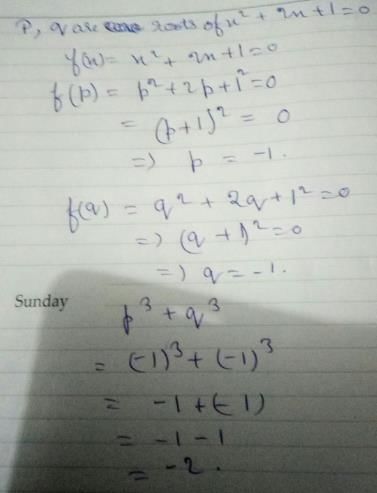Test: Equations- 2 - CA Foundation MCQ
30 Questions MCQ Test - Test: Equations- 2
Monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenses are in the ratio 7 : 9. If each saves Rs. 50 per month find their monthly incomes.
Find the fraction which is equal to 1/2 when both its numerator and denominator are increased by 2. It is equal to 3/4 when both are incresed by 12.
The age of a person is twice the sum of the ages of his two sons and five years ago his age was thrice the sum of their ages. Find his present age.
A number between 10 and 100 is five times the sum of its digits. If 9 be added to it the digits are reversed find the number.
The wages of 8 men and 6 boys amount to Rs. 33. If 4 men earn Rs. 4.50 more than 5 boys determine the wages of each man and boy.
A number consisting of two digits is four times the sum of its digits and if 27 be added to it the digits are reversed. The number is :
Of two numbers, 1/5th of the greater is equal to 1/3rd of the smaller and their sum is 16.The numbers are:
Y is older than x by 7 years 15 years back X’s age was 3/4 of Y’s age. Their present ages are:
The sum of the digits in a three digit number is 12. if the digits are reversedthe number is increased by 495 but reversing only of ten’s and the unit digits increases the number by 36
Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are :
The demand and supply equations for a certain commodity are 4q + 7p = 17 and respectively where p is the market price and q is the quantity then the equilibrium price and quantity are:
If the roots of the equation 2x2 + 8x – m3 = 0 are equal then value of m is
The cost of 10 kg of apples is equal to the cost of 24 kg of rice. The cost of 6 kg of flour equals the cost of 2 kg of rice. The cost of each kg of flour is Rs.20.50. Find the total cost of 4 kg of apples, 3 kg of rice and 5 kg of flour?
If œ ß be the roots of the equation 2x2 – 4x – 3 = 0 the value of α2 + β2 is
If the sum of the roots of the quadratic equation ax2 + bx + c = 0 is equal to the sum of the squares of their reciprocals then
The equation x2 –(p+4)x + 2p + 5 = 0 has equal roots the values of p will be.
If x = m is one of the solutions of the equation 2x2 + 5x – m = 0 the possible values of m are
If p and q are the roots of x2 + 2x + 1 = 0 then the values of p3 + q3 becomes
If L + M + N = 0 and L M N are rationals the roots of the equation (M+N–L) x2 + (N+L–M)x + (L+M–N) = 0 are
If p ≠ q and p2 = 5p – 3 and q2 = 5q – 3 the equation having roots as
If one rot of 5x2 + 13x + p = 0 be reciprocal of the other then the value of p is
A solution of the quadratic equation (a+b–2c)x2 + (2a–b–c)x + (c+a–2b) = 0 is
If the root of the equation x2–8x+m = 0 exceeds the other by 4 then the value of m is
The values of x in the equation 7(x+2p)2 + 5p2 = 35xp + 117p2 are