We label by ai the probability that, starting in state i, the chain is eventually absorbed in the closed set {0,3}. Since {0,3} is closed,
-
a₀ = 1 (if you start in 0 you’re already in {0,3}),
-
a₃ = 1,
and the other closed state 1 lies outside our target class, so -
a₁ = 0.
States 2 and 4 are transient, and satisfy the usual linear equations
a₂ = P(2→0)·a₀ + P(2→1)·a₁
a₄ = Σₖ P(4→k)·aₖ.
From the matrix row for state 2, P(2→0)=1/3, P(2→1)=2/3, and no chance to go directly to 3 or 4. Hence
a₂ = (1/3)·1 + (2/3)·0 = 1/3.
From the row for state 4, the transitions are
-
to 0 with probability 1/8,
-
to 1 with probability 1/8,
-
to 2 with probability 1/2,
-
to 3 with probability 1/8,
-
to 4 itself with probability 1/8.
Thus
a₄ = (1/8)·a₀ + (1/8)·a₁ + (1/2)·a₂ + (1/8)·a₃ + (1/8)·a₄
Substitute a₀=1, a₁=0, a₂=1/3, a₃=1:
a₄ = 1/8 + 0 + (1/2)·(1/3) + 1/8 + (1/8)·a₄
a₄ = 1/8 + 1/6 + 1/8 + (1/8)a₄
Combine the constants: 1/8+1/8 =1/4, and 1/4+1/6 = (3/12+2/12)=5/12, so
a₄ = 5/12 + (1/8)·a₄
Bring the a₄–term to the left:
a₄·(1 – 1/8) = 5/12
(7/8)·a₄ = 5/12
a₄ = (5/12)·(8/7) = 40/84 = 10/21.
Hence starting from state 4 the probability of eventual absorption in {0,3} is 10/21.


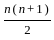
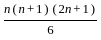
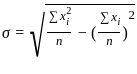
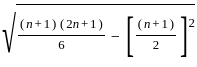
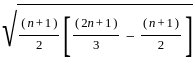
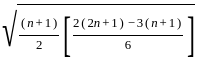
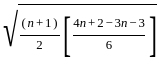
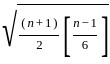
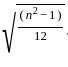
 ≈ 2.87
≈ 2.87
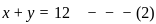
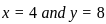
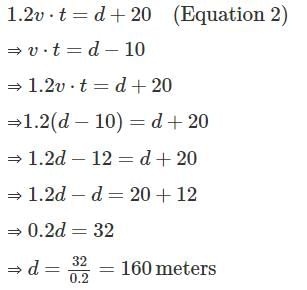
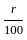 )n
)n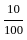 )3 = 150000(1 + 0.1)3 = 150000(1.1)3 = 199650
)3 = 150000(1 + 0.1)3 = 150000(1.1)3 = 199650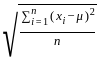

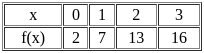

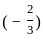 + (x - 0)(x - 1)(x - 2)(x - 3)
+ (x - 0)(x - 1)(x - 2)(x - 3)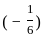
 = 1/3
= 1/3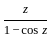 ) has
) has  exist
exist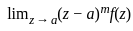 ≠ 0
≠ 0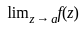 does not exist
does not exist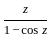 )
)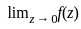 =
=  (0/0 form)
(0/0 form) 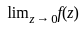 =
= 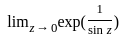 , does not exist
, does not exist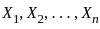 be i.i.d.(independent and identically distributed) random variables with uniform distribution on the interval [0, 1]. Let
be i.i.d.(independent and identically distributed) random variables with uniform distribution on the interval [0, 1]. Let 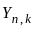 denote the kth order statistic based on the sample
denote the kth order statistic based on the sample 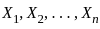 . If we select two different samples of size 25 and 26, denoted as
. If we select two different samples of size 25 and 26, denoted as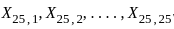 and
and 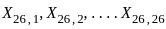 respectively, and let Y be the 8th order statistic in both samples. What is the probability that
respectively, and let Y be the 8th order statistic in both samples. What is the probability that  ?
?
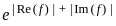 is bounded, then f is constant.
is bounded, then f is constant.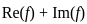 and the product
and the product 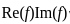 are bounded, then f is constant.
are bounded, then f is constant.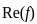 and
and  imposes significant restrictions on the behavior of f. If both these quantities are bounded, then f must be constant.
imposes significant restrictions on the behavior of f. If both these quantities are bounded, then f must be constant.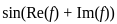 is bounded, then f is constant.
is bounded, then f is constant.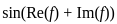 does not necessarily imply that f is constant. The function f could still vary without violating this condition.
does not necessarily imply that f is constant. The function f could still vary without violating this condition.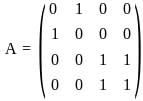 and consider the symmetric bilinear form on R4 given by (v, w) = vt Aw, for v, w ∈ ℝ4. Which of the following statements is true?
and consider the symmetric bilinear form on R4 given by (v, w) = vt Aw, for v, w ∈ ℝ4. Which of the following statements is true?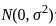 , the expression
, the expression 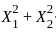 follows a chi-squared distribution with 2 degrees of freedom, scaled by σ2 :
follows a chi-squared distribution with 2 degrees of freedom, scaled by σ2 :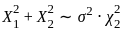
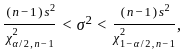 where s2 is the sample variance.
where s2 is the sample variance. and
and 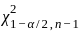 are the critical values from the chi-squared distribution with n-1 degrees of freedom.
are the critical values from the chi-squared distribution with n-1 degrees of freedom. , where
, where 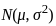 denotes a normal distribution with mean μ and variance σ2 .
denotes a normal distribution with mean μ and variance σ2 .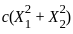 , where this expression helps define a confidence interval.
, where this expression helps define a confidence interval.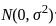 , their squares follow a chi-squared distribution with 2 degrees of freedom, scaled by σ2 . Specifically
, their squares follow a chi-squared distribution with 2 degrees of freedom, scaled by σ2 . Specifically 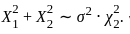
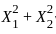 can be used to construct a confidence interval for the variance σ2.
can be used to construct a confidence interval for the variance σ2.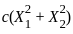 is related to the chi-squared distribution. The confidence interval is based on the quantiles of the chi-squared distribution. For a 95% confidence interval, the confidence coefficient is 0.95, which means we need the quantiles of the chi-squared distribution at 5% significance level (0.05).
is related to the chi-squared distribution. The confidence interval is based on the quantiles of the chi-squared distribution. For a 95% confidence interval, the confidence coefficient is 0.95, which means we need the quantiles of the chi-squared distribution at 5% significance level (0.05).
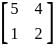 .
.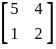
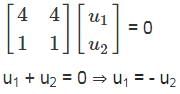
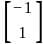
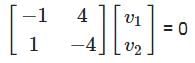

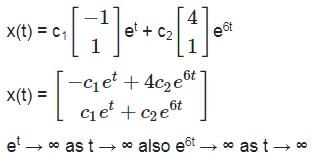
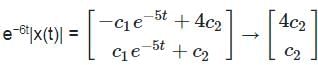
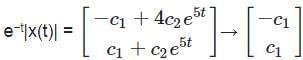
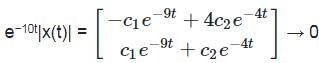
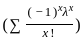 = e
= e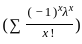
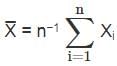 denotes the sample mean and let t0.975, n−1 denote the 0.975-quantile of a Student's− t distribution with n − 1 degrees of freedom. Which of the following statements is true for the following interval
denotes the sample mean and let t0.975, n−1 denote the 0.975-quantile of a Student's− t distribution with n − 1 degrees of freedom. Which of the following statements is true for the following interval  ?
?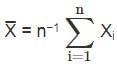
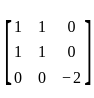
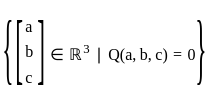 .
.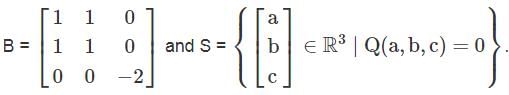
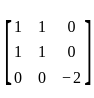
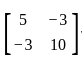
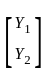 is E(Y) =
is E(Y) = 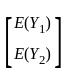 and covariance matrix of Y is Σ =
and covariance matrix of Y is Σ = 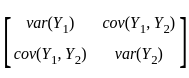
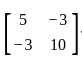
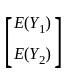 =
= 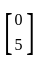 .......(v)
.......(v)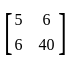
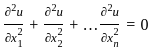
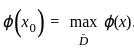
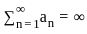 then the series
then the series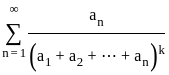 is
is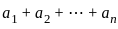 then
then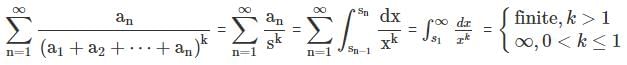
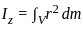 , where r is the perpendicular distance from the z -axis, dm = ρdV is the mass element and ρ is the constant density. For this particular geometry, we are revolving the disc described by the equation
, where r is the perpendicular distance from the z -axis, dm = ρdV is the mass element and ρ is the constant density. For this particular geometry, we are revolving the disc described by the equation 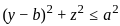 around the z - axis, where
around the z - axis, where 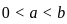 .
.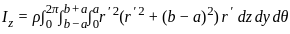
 , a space is compact if every open cover has a finite subcover. Since the cofinite topology ensures that every cover must have at least one large set with a finite complement, X is compact.
, a space is compact if every open cover has a finite subcover. Since the cofinite topology ensures that every cover must have at least one large set with a finite complement, X is compact.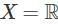 with the Euclidean topology is not compact (since
with the Euclidean topology is not compact (since 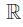 is not bounded or closed in the Euclidean topology).
is not bounded or closed in the Euclidean topology).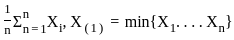 and X(n) = max {X1....., Xn}. Which of the following statements are true?
and X(n) = max {X1....., Xn}. Which of the following statements are true?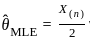 , where X(n) is the maximum value in the sample.
, where X(n) is the maximum value in the sample.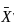 equal to the theoretical mean, we solve for θ.
equal to the theoretical mean, we solve for θ.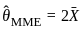 , where
, where  is the sample mean.
is the sample mean.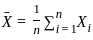 is the sample mean.
is the sample mean.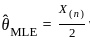
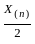 and taking the maximum with -X(1) could ensure that the parameter is positive.
and taking the maximum with -X(1) could ensure that the parameter is positive.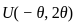 distribution is:
distribution is: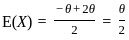
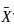 , we get,
, we get,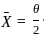

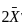 , not
, not  .
.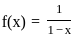 , For n ≥ 1, let pn(x) = 1 + x + ....+ xn, Then which of the following statements are true?
, For n ≥ 1, let pn(x) = 1 + x + ....+ xn, Then which of the following statements are true?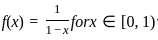
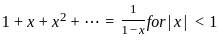 , which means pn(x) is an approximation of f(x) as n → ∞.
, which means pn(x) is an approximation of f(x) as n → ∞. blows up as x → 1, meaning that as we get closer to 1, the function value grows without bound. This implies that f(x) is not uniformly continuous because the difference in function values for close inputs near 1 can be arbitrarily large.
blows up as x → 1, meaning that as we get closer to 1, the function value grows without bound. This implies that f(x) is not uniformly continuous because the difference in function values for close inputs near 1 can be arbitrarily large.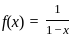 . Therefore, pn(x) converges to f(x) pointwise on [0, 1).
. Therefore, pn(x) converges to f(x) pointwise on [0, 1).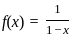 is continuous and well-behaved on the interval [0, c], and the sequence pn(x) will converge uniformly on compact subintervals away from 1.
is continuous and well-behaved on the interval [0, c], and the sequence pn(x) will converge uniformly on compact subintervals away from 1.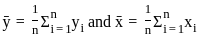 ; are observed sample means. Under squared error loss function, which of the following statements are true?
; are observed sample means. Under squared error loss function, which of the following statements are true?










