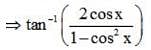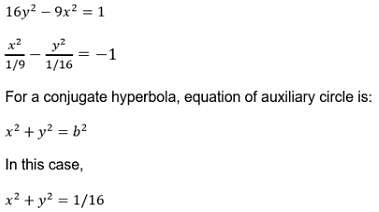KVS PGT Mathematics Mock Test - 1 - KVS PGT/TGT/PRT MCQ
30 Questions MCQ Test KVS PGT Exam Mock Test Series 2024 - KVS PGT Mathematics Mock Test - 1
Directions: In the following question, one part of the sentence may have error(s). Find out the part of the sentence having an error and select the appropriate option. If a sentence is free from error, select 'No error' as your answer.
Q. He admitted/(1) that he /(2) had written the letter./(3) No error (4)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Select the option which is related to the third term in the same way as the second term is related to the first term.
Synonym : Similar :: Opposite : ?
The curriculum organization which gives scope for both ‘principle of difficulty’ and ‘principle of repetition’ in the same class is
Community participation in school culture is essential because ________
Let X = {x | x = 2 + 4k, where k = 0, 1, 2, 3,...24}. Let S be a subset of X such that the sum of no two elements of S is 100. What is the maximum possible number of elements in S ?
Find the projection of the vector on the vector
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have coordinates (3, 4) and (–4, 3) respectively, then ∠QPR may be equal to
If A = {1, 3, 4} and B = {1, 4, 3, 2} then which of the following is true?
Consider the following statements:
I: If A = {x: x is an even natural number} and B = {y: y is a natural number}, A subset B.
II: Number of subsets for the given set A = {5, 6, 7, 8) is 15.
III: Number of proper subsets for the given set A = {5, 6, 7, 8) is 15.
Which of the following statement(s) is/are correct?
If “a” is the first term and ℓ is the last term (nth term), then the sum of all the term of this sequence is given by:
The line x + y = 6 is a normal to the parabola y2 = 8x at the point
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is
If n (P) = 5, n(Q) = 12 and n(P U Q) = 14 then n(P ∩ Q) =
A coin is tossed n times. The probability of getting head at least once is greater than 0.8. Then the least value of n is
The …… of a conic is the chord passing through the focus and perpendicular to the axis.
Locus of the feet of the perpendiculars drawn from either foci on a variable tangent to the hyperbola 16y2 – 9x2 = 1 is
Two students while solving a quadratic equation in x, one copied the constant term incorrectly and got the roots as 3 and 2. The other copied correctly the constant term and coefficient of x2 as -6 and 1 respectively. The correct roots are
Degree of a differential equation, when the equation is polynomial equation in y′ is



 equlas
equlas