TN TRB PG Assistant Mock Test- 1 (Mathematics) - TN TET MCQ
30 Questions MCQ Test TN TRB PG Assistant Mock Test Series 2025 - TN TRB PG Assistant Mock Test- 1 (Mathematics)
Evaluate  for
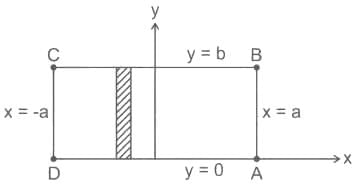
for 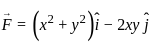 taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.
taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.
 for
for 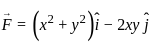 taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.
taken around the rectangle bounded by the lines x = ± a, y = 0, y = b.Suppose f ; ℝ→ℝ is an odd and differentiable fraction. Then for every x0 ∈ ℝ. f'(-x0) is equal to;
The divergence of the vector field 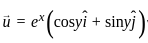 is
is
If C is any simple closed curve enclosing the point z = z0, then the value of 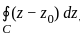
If R→R is given by f(x) = x3 + x2f'(1) + xf''(2) + f'''(3) for all x in R. then f(2) - f(1) is
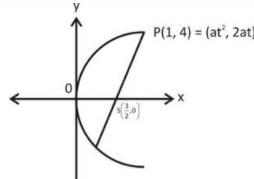
If one end of a focal chord of the parabola, y2 = 16x is at (1, 4), then the length of this focal chord is:
Given f (x) = ex cosy, what is the value of the fifth term in Taylor's series near (1, π/4) where it is expanded in increasing order of degree & by following algebraic identity rule?
Let f be the function on [0, 1] defined by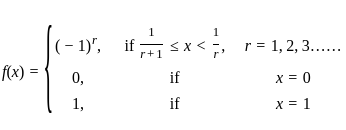 then which of the following is/are) correct:
then which of the following is/are) correct:
(A) f(x) is continuous at x = 1/2
(B) f(x) is continuous on [0, 1].
(C) f(x) is discontinuous at 1/2.
(D) f(x) is continuous on (1/2, 1)
Choose the correct answer from the options given below:
What is cofactor of 7 for the determinant given below:

The function f(x) = (4 - x²) / (4x - x³) is
Let A be an n-by-n matrix with coefficients in F, having rows{a1, ..., an). Then which one of the statement is true for the matrix A?
Given a square matrix A which of the following will always be true?
(I). AᵀA = AAᵀ
(II). A - Aᵀ is skew symmetric
(III). A⁻¹ exists
(IV). (Aᵀ)⁻¹ = (A⁻¹)ᵀ
Y = (x + 2)(x – 1) (x + 3) find dy/dx
Let S be a closed surface and let denote the position vector of any point (x,y,z) measured from an origin O. then 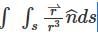 is equal to (if O lies inside S).
is equal to (if O lies inside S).
Let V be the vector space of real polynomials of degree atmost 2. which defines a linear operator 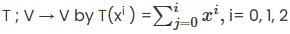 then the matrix of T–1 with respect to the basis (1, x, x2 ) is
then the matrix of T–1 with respect to the basis (1, x, x2 ) is
Let  denote the eigenvalues of the matrix
denote the eigenvalues of the matrix 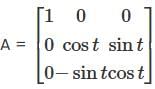
If  , then the set of possible values of t, -π ≤ t < π, is
, then the set of possible values of t, -π ≤ t < π, is
While cutting, if the plane is at an angle and it cuts all the generators, then the conic formed is called as ______
Choose a number n uniformly at random from the set {1,2,…,100}. Choose one of the first seven days of the year 2014 at random and consider n consecutive days starting from the chosen day. What is the probability that among the chosen �� days, the number of Sundays is different from the number of Mondays?
Define the function f : ℝ2 → ℝ by
f(x, y) = 12xy e−(2x + 3y − 2).
If (a, b) is the point of local maximum of f, then f(a, b) equals
Statement (B): It prioritizes top-down planning by educational policymakers.


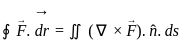
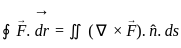
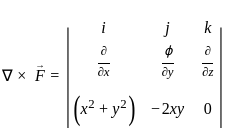
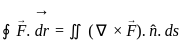
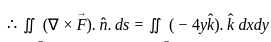
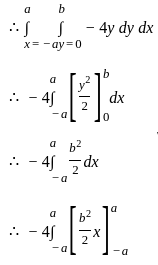

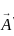 is defined as:
is defined as: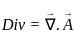
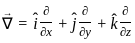
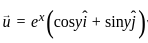
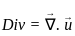
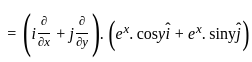
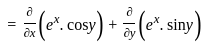
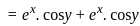
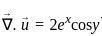
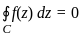

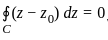
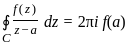
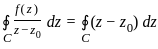
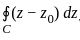 is
is
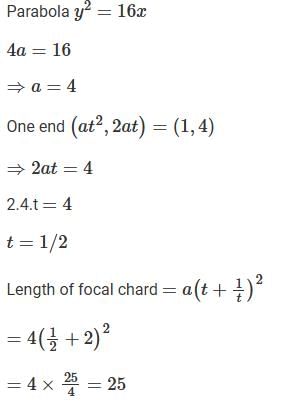
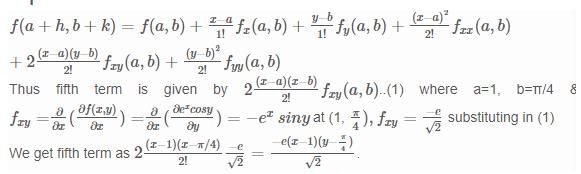
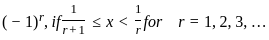 ,
,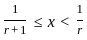
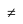 RHL at x = 1/2
RHL at x = 1/2 ,
,

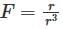 has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε.
has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε. 
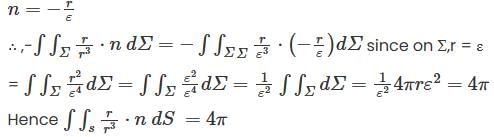
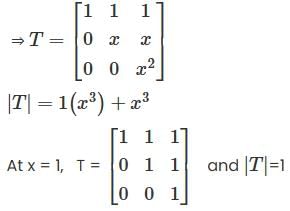
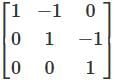

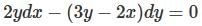 is:
is: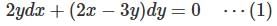
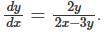
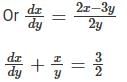
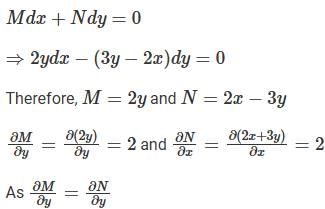

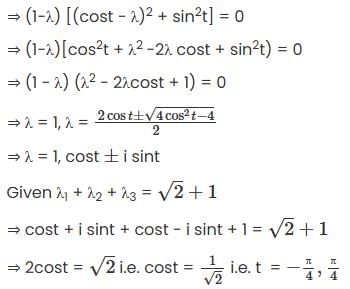
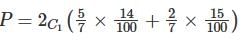
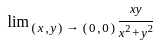 is :
is :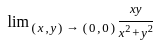
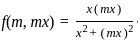
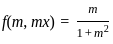
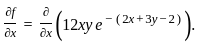
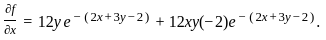
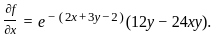

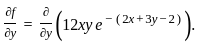
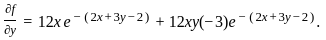
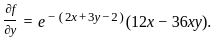
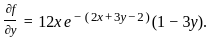
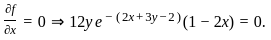
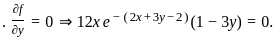
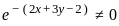 , we get the conditions:
, we get the conditions: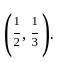 .
.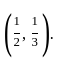
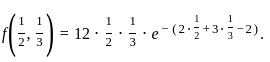
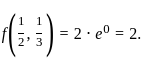
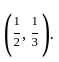 is 2.
is 2.










