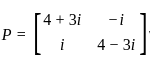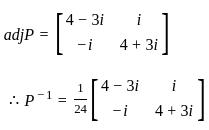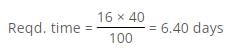TN TRB PG Assistant Mock Test- 2 (Mathematics) - TN TET MCQ
30 Questions MCQ Test TN TRB PG Assistant Mock Test Series 2025 - TN TRB PG Assistant Mock Test- 2 (Mathematics)
If f and g be continuous real valued functions on the metric space M. Let A be the set of all x ∈ M s.t. f(x) < g(x)
The function f : ℝ ℝ → satisfied  for all x, y ∈ and some constant c ∈ Then,
for all x, y ∈ and some constant c ∈ Then,
 for all x, y ∈ and some constant c ∈ Then,
for all x, y ∈ and some constant c ∈ Then, The function sinx (1 + cosx) at x = π/3 is
Determine the logarithmic function of ln(1 + 5x)-5
Consider the f(x, y) = x2 + y2 – a. For what values of a do we have critical points for the function
Which one of the following is the differential equation that represents the family of curves 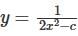 where c is an arbitrary constant?
where c is an arbitrary constant?
The point (0,0) in the domain of f(x, y) = sin(xy) is a point of
If A, B, C are square matrices of the same order, then which of the following is true?
 where F(x, y, z) = (y + z, z + x, x + y)
where F(x, y, z) = (y + z, z + x, x + y)
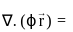 will be _______, where
will be _______, where 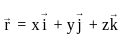
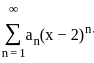 converges at x = -5. Then this series also converges at
converges at x = -5. Then this series also converges at
Consider the Linear Programming Problem (LPP):
Maximize z = 2x + y
subject to the constraints:
3x - 7y ≤ 21
y - 2x ≤ 10
x, y ≥ 0. Then
Match List-I with List-II

Choose the correct answer from the options given below:
Which of the following are true?
(A) Let G = <a> be a cyclic group of order n, then G = <ak> if and only if gcd(k, n) = 1
(B) Let G be a group and let a be an element of order n in G. If ak = e, then n divides k.
(C) The centre of a group G may not be a subgroup of the group G.
(D) For each 'a' in a group G, the centralizer of 'a' is a subgroup of group G
Choose the correct answer from the options given below:
Which of the following is/are) correct:
A. If U = x2 - y2 is real part of an analytic function f(z) then analytic function f(z) = z + c
B. Zeros of cosz is 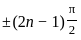 , where n = 1, 2, 3,
, where n = 1, 2, 3,
C. If f is entire and bounded for all values of z in the complex plane, then f(z) is constant throughout the plane.
D.  = πi, where |z| =
= πi, where |z| = 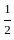
Choose the correct answer from the options given below:
The unit normal vector to the surface X² + Y² + Z² - 48 = 0 at the point (4, 4, 4) is:
A conditionally convergent series is a series which is -
For a given matrix P = 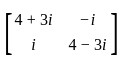 , where i = √-1, the inverse of matrix P is
, where i = √-1, the inverse of matrix P is
While working with 40% of his efficiency a man can complete a work in 16 days. In how many days can he complete the work while working with 100% efficiency?



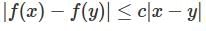
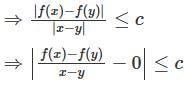

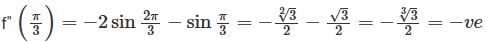
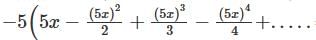
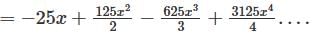
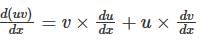
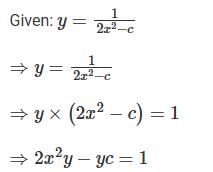
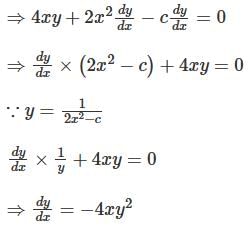
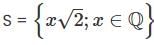 then the closure of S is
then the closure of S is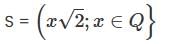
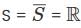 Which is uncountable
Which is uncountable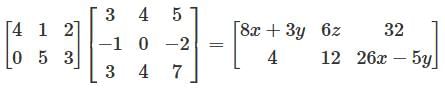 then find the value of x, y, z
then find the value of x, y, z 
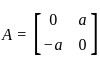
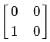 and B =
and B =  then also = AB = 0
then also = AB = 0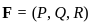 is given by the vector cross product of the del operator with
is given by the vector cross product of the del operator with 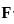 , i.e.,
, i.e., 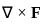 . It is computed as:
. It is computed as: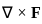 =
= 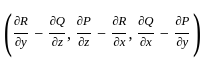
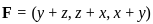 .
.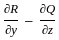 :
: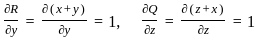
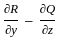 = 1 - 1 = 0
= 1 - 1 = 0 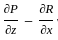 :
: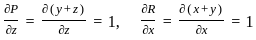
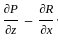 = 1 - 1 = 0
= 1 - 1 = 0 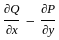 :
: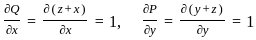
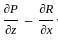
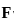 is:
is: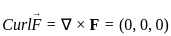
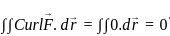
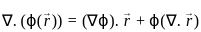
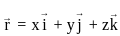
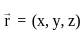 &
& 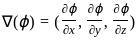
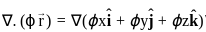
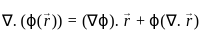
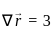
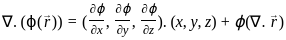
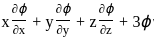
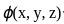 is homogenous function of degree 4,
is homogenous function of degree 4, 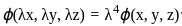
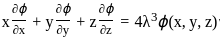
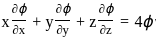
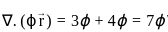
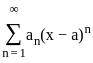 converges at x = x0, then it also converges at all the values of x for which the following inequality is satisfied:
converges at x = x0, then it also converges at all the values of x for which the following inequality is satisfied: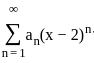 converges at x = - 5
converges at x = - 5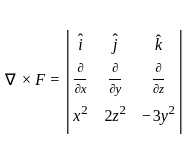
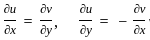

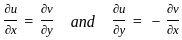 , we get:
, we get: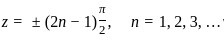
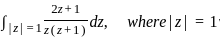
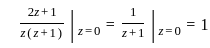
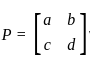 then |P| = (a × d) - (b × c)
then |P| = (a × d) - (b × c)