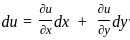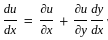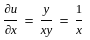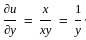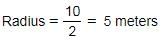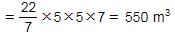TN TRB PG Assistant Mock Test- 3 (Mathematics) - TN TET MCQ
30 Questions MCQ Test TN TRB PG Assistant Mock Test Series 2025 - TN TRB PG Assistant Mock Test- 3 (Mathematics)
Computation of the discrete logarithm is the basis of the cryptographic system _______
Convert the (10, 90, 60) coordinates to Cartesian coordinates which are in Spherical coordinates.
If ‘p’, ‘q’ and ‘n’ are probability pf success, failure and number of trials respectively in a Binomial Distribution, what is its Standard Deviation ?
Let T: R3 → R3 be the Linear transformation whose matrix with respect to the standard basis 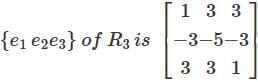 Then T
Then T
Let V be the vector space of function 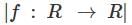 if W be its subsets then which of the following W is subspace of v
if W be its subsets then which of the following W is subspace of v
Consider a system of linear equations Ax = b, where
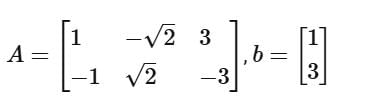
This system is equations admits __________.
The mass of a solid right circular cylinder of height h and radius of base b, if density (mass per unit volume) is numerically equal to the square of the distance from the axis of the cylinder.is
Consider the series
∑ (from n=3 to ∞) aⁿ / (nᵇ (logₑ n)ᶜ)
For which values of a, b, c ∈ ℝ, does the series NOT converge?
Let S denote the set of all real numbers except -1. Define the binary operation'' on S as a b = a + b + ab. Then the solution of the equation 2* x * 3 = 7 is
Which of the following statement is not correct?
For which value of k, the function f(x) = 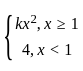 is continuous at x = 1?
is continuous at x = 1?
lim (n→∞) (n! / ((n+1)! + n!)) = ?
Function f(x) = (x + 1)cotx will be continuous at x = 0 if the value of f(0) is
Let A be a symmetric matrix of order 2 with integer entries. If the sum of the diagonal elements of A2 is 1, then the possible number of such matrices is :
 be a sequence of positive real number such that
be a sequence of positive real number such that 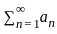 is divergent. Which of the following is true?
is divergent. Which of the following is true?
Let F be the family of curves given by
x2 + 2hxy + y2 = 1, − 1 < h < 1 .
Then, the differential equation for the family of orthogonal trajectories to F is
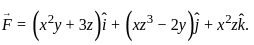 Then the value of grad(div
Then the value of grad(div 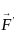 ) at the point (1, 2, 3) is
) at the point (1, 2, 3) is
Consider two rings R = Z/4Z, and S = Z/12Z, then how many distinct ring homomorphisms φ: R → S exist?
Let f = yx. What is 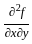 at x = 2, y = 1?
at x = 2, y = 1?
The sequence {Xn}, where Xn = 1 + 1/3 + 1/5 + __ __ + 1/(2n - 1) is
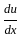 = ?
= ?
Which of the following is a subspace of R3?
What is the volume of a cylinder with 10 meters of diameter and 7 meters of height?
In a college, the ratio of the number of boys to the number of girls is 5 : 3. If 80 boys leave the college and 40 girls join the college, the number of the girls will become the same as the number of boys. What is the initial number of boys in the college?




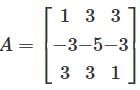
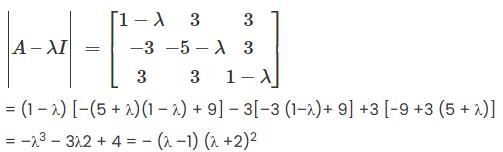
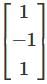
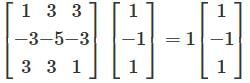
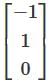
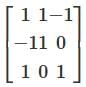

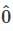 denote the zero polynomial, so
denote the zero polynomial, so  for every value of x.
for every value of x.  ∈ W, since
∈ W, since 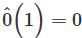 Suppose f. g ∈ W. Then f(1) = 0 and g(1) = 0. Also, for scalars a and b, we have
Suppose f. g ∈ W. Then f(1) = 0 and g(1) = 0. Also, for scalars a and b, we have 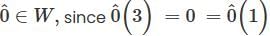 . Suppose f, g ∈ W. Them f(3) = f(1) and g(3) g(1). Thus, for any scalars a and b, we have
. Suppose f, g ∈ W. Them f(3) = f(1) and g(3) g(1). Thus, for any scalars a and b, we have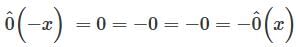 . Suppose f . g ∈ W. Then f(–x) = –f(x) and g(–x) = –g(x).
. Suppose f . g ∈ W. Then f(–x) = –f(x) and g(–x) = –g(x). 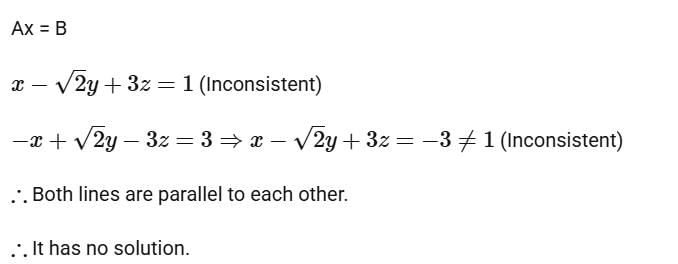
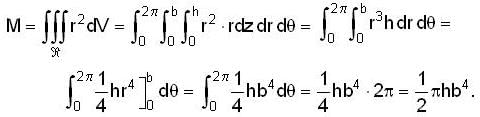
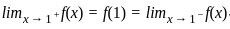
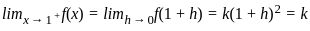
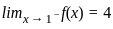
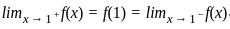
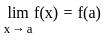
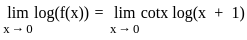
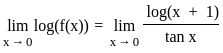 = 0/0 form
= 0/0 form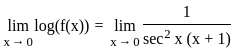
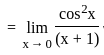
 converges if
converges if 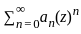 is then
is then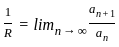
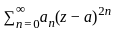 then
then 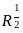
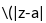
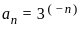
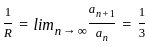

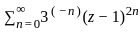 is
is 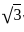
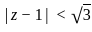
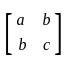
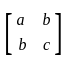
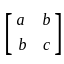
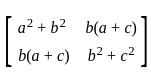
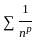 is convergent for p > 1
is convergent for p > 1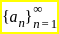 be a sequence of positive real number such that
be a sequence of positive real number such that 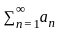 is divergent.
is divergent.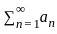 is divergent
is divergent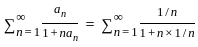
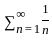 is divergent series by p - test.
is divergent series by p - test.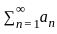 is divergent
is divergent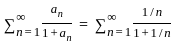
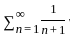 is divergent series by p - test.
is divergent series by p - test.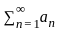
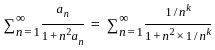

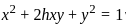 , − 1 < h < 1 .
, − 1 < h < 1 .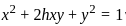
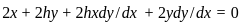
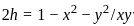
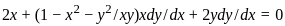
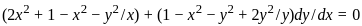
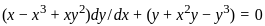
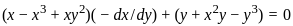
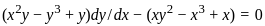
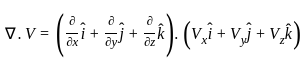
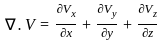
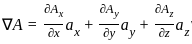
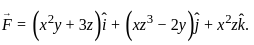
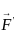 :
: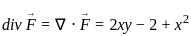
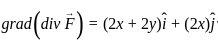
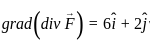
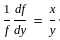
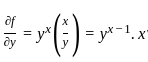
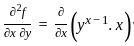
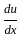 is given by:
is given by: