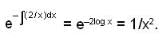TN TRB PG Assistant Mock Test- 5 (Mathematics) - TN TET MCQ
30 Questions MCQ Test TN TRB PG Assistant Mock Test Series 2025 - TN TRB PG Assistant Mock Test- 5 (Mathematics)
A commutative group G is simple if and only if-
If R is the radius of convergence of any power series then what is the interval of convergence?
Which of the following statement is NOT true?
Consider the linear programming problem (LPP)
Maximize Z = -x1 + 4x2,
subject to 3x1 - x2 ≥ -3,
-0.3x1 + 1.2x2 ≤ 3,
x1, x2 ≥ 0. then which of the following is correct?
Which of the following statements is necessarily true for a commutative ring R with unity?
If C is a skew-symmetric matrix of order n and X is n × 1 column matrix, then XT CX is a
For the function f(z) = z2, the value of derivative at z = 4 is
The value of integral 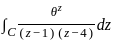 , where C is the circle |z| = 2 is
, where C is the circle |z| = 2 is
The area of the portion of the surface z = x2 - y2 in R3 which lies inside the solid cylinder x2 + y2 ≤ 1 is
The specific integral of the equation (D2 - D'2 + D - D') Z = e2x+3y will be _______.
Let W be a solution space of the differential equation 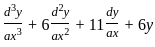 = 0. Then dimension of the solution space W is
= 0. Then dimension of the solution space W is
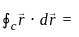 ________
________
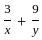 is:
is:
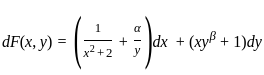 an exact differential equation?
an exact differential equation?
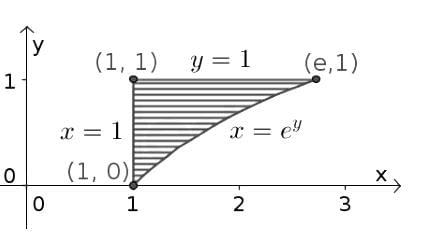
Change the order of integration in the following integral
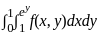 =
= 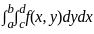
Then find the value of e(a - d) ____
If G is a group, Z its center and if G/Z is cyclic then G
Let N1 and N2 be two normal subgroup of a group G then 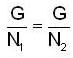 if
if
Solution of the differential equation 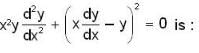
Statement (B): It is used exclusively for financial management in educational institutions.


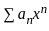 then the series converges when |x| < R i.e., when - R < x < R
then the series converges when |x| < R i.e., when - R < x < R
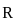
 .
.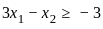 ⟶ equivalently:
⟶ equivalently: 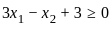
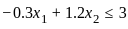 (no change needed)
(no change needed)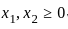 (Non-negativity constraints)
(Non-negativity constraints)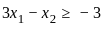 to equality:
to equality: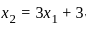 ----------------(1)
----------------(1)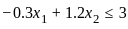 to equality:
to equality: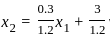
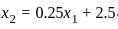 --------------(2)
--------------(2)
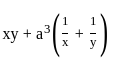 is
is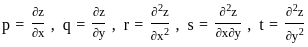 for the given function
for the given function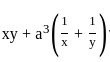
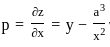 and
and 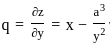
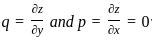 and solving two equations we get
and solving two equations we get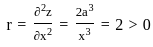 ,
, 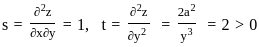
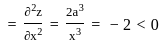 ,
, 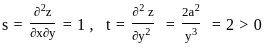
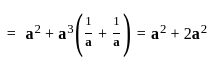 = 3a2.
= 3a2.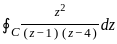 where C is the circle |z| = 2
where C is the circle |z| = 2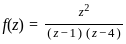 at z = 1 , we express it in the form:
at z = 1 , we express it in the form: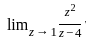
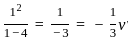
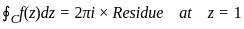
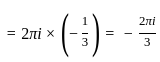
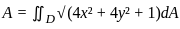
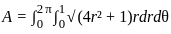
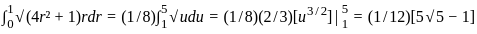
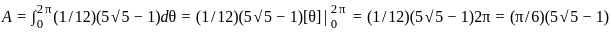
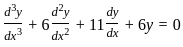
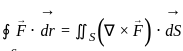 , where
, where 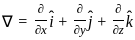
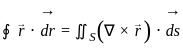
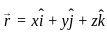
 = 0
= 0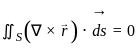

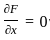
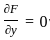
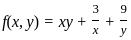
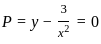 ........(i)
........(i)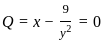 ............(ii)
............(ii)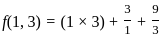
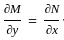
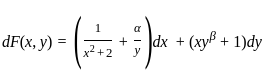
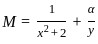 and
and 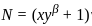
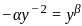
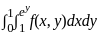
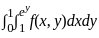
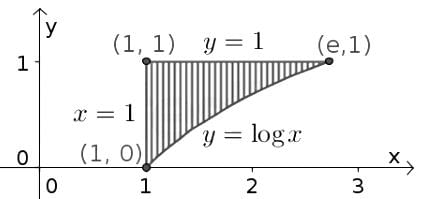
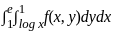
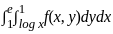 =
= 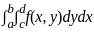
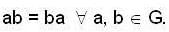
 z1 ∈ Z such that a ∈ z1 gm
z1 ∈ Z such that a ∈ z1 gm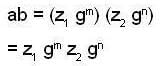
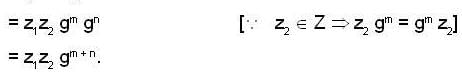 Again
Again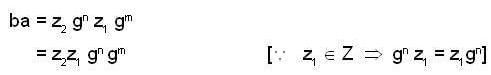
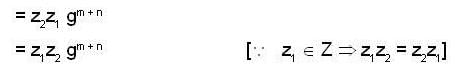
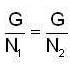 then we are to prove that N1 = N2 we have
then we are to prove that N1 = N2 we have 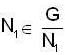 but
but 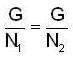 therefore
therefore 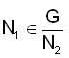 that is N1 is equal to some coset of N2 in G. But two cosets of N2 in G are either disjoint or identical since e ∈ N1 and e ∈ N2 th e re fo re N1 and N2 are not disjoint so we must have N1 = N2.
that is N1 is equal to some coset of N2 in G. But two cosets of N2 in G are either disjoint or identical since e ∈ N1 and e ∈ N2 th e re fo re N1 and N2 are not disjoint so we must have N1 = N2.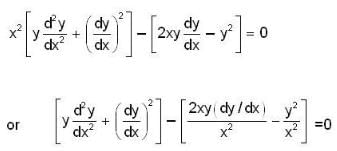

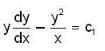
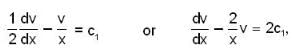 which is linear. Its I.F =
which is linear. Its I.F =