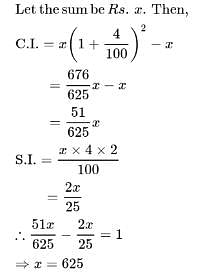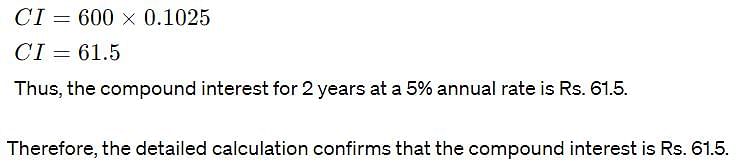Test: Compound Interest- 1 - UPSC MCQ
10 Questions MCQ Test CSAT Preparation - Test: Compound Interest- 1
Q. What is the difference between the compound interests on Rs. 5000 for 11/2 years at 4 percent per annum compounded yearly and half yearly?
A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs. 1600 each on 1st January and 1st July of a year. At the end of the year, the amount he would have gained by way of interest is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
There is 80% increase in an amount in 8 years at simple interest. What will be the compound interest of Rs. 14,000 after 3 years at the same rate?
The compound interest on Rs. 30,000 at 7% per annum is Rs. 4347. The period (in years) is:
The difference between simple and compound interests compounded annually on a certain sum of money for 2 years at 4% per annum is Re. 1. The sum is:
The difference between compound interest and simple interest on an amount of Rs. 15,000 for 2 years is Rs. 96. What is the rate of interest per annum?
If the simple interest on a sum of money for 2 years at 5% per annum is Rs. 60, what is the compound interest on the same at the same rate and for the same time?
The difference between simple interest and compound on Rs. 900 for one year at 10% per annum reckoned half-yearly is:
What will be the compound interest on a sum of Rs. 40,000 after 3 years at the rate of 11 p.c.p.a.?
At what rate of compound interest per annum will a sum of Rs. 1400 become Rs. 1573.04 in 2 years?
|
218 videos|139 docs|151 tests
|