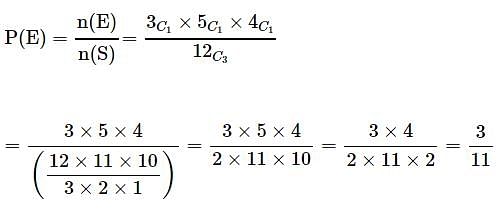Test: Probability- 2 - UPSC MCQ
10 Questions MCQ Test CSAT Preparation - Test: Probability- 2
What is the probability of selecting a prime number from 1,2,3,... 10 ?
3 balls are drawn randomly from a bag contains 3 black, 5 red and 4 blue balls. What is the probability that the balls drawn contain balls of different colors?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
5 coins are tossed together. What is the probability of getting exactly 2 heads?
What is the probability of drawing a "Queen" from a deck of 52 cards?
A card is randomly drawn from a deck of 52 cards. What is the probability getting an Ace or King or Queen?
A card is randomly drawn from a deck of 52 cards. What is the probability getting a five of Spade or Club?
When two dice are rolled, what is the probability that the sum is either 7 or 11?
A card is randomly drawn from a deck of 52 cards. What is the probability getting either a King or a Diamond?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that none of them are selected?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that only one of them is selected?
|
218 videos|139 docs|151 tests
|